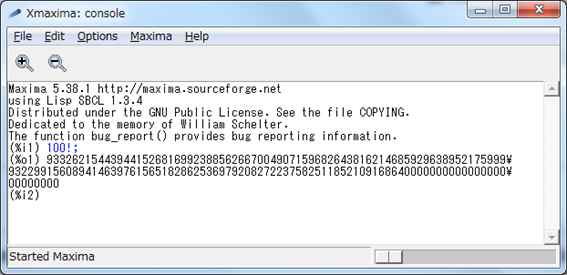
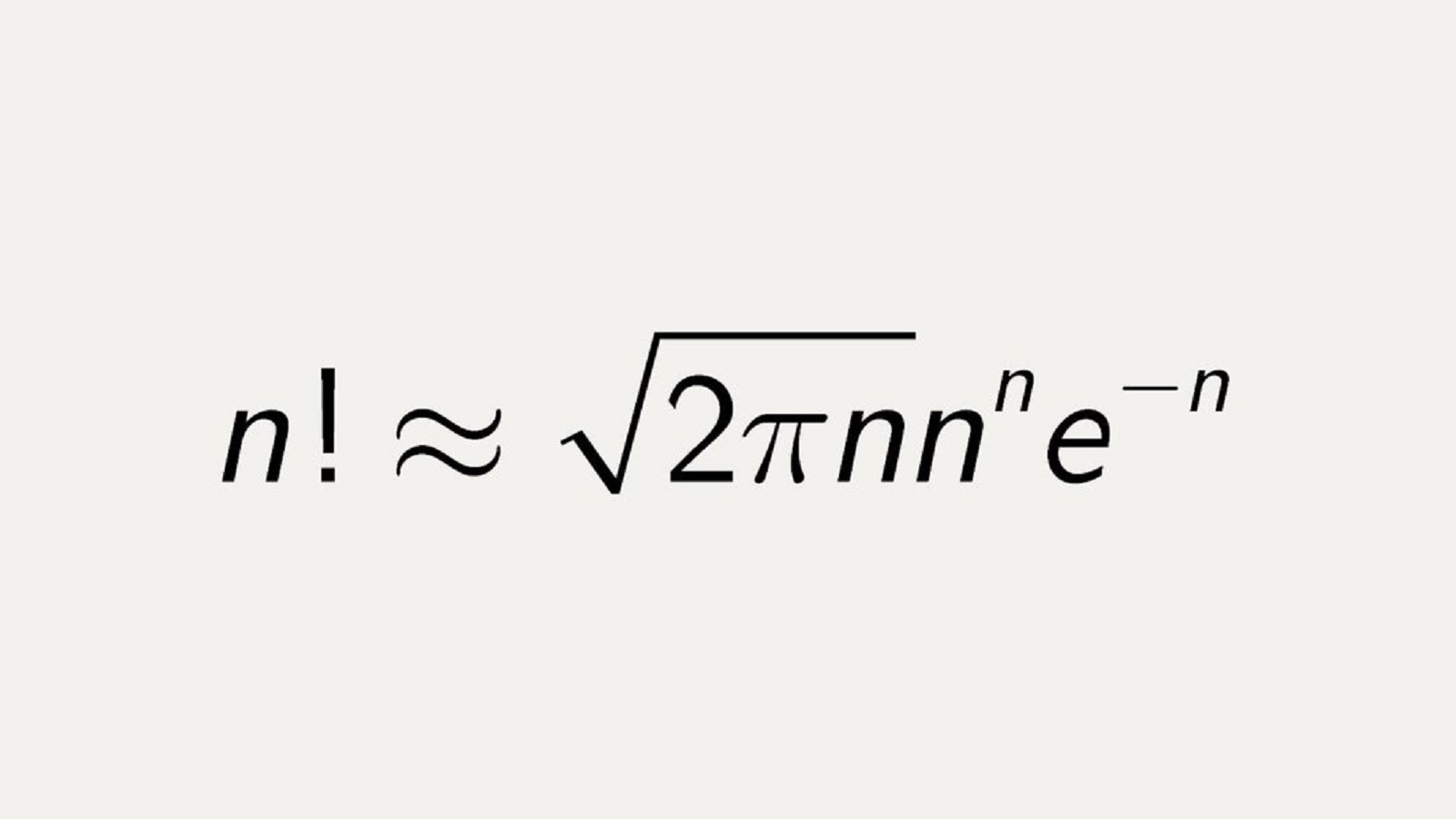Berapakah nilai dari 100! (seratus faktorial)? Nilai faktorial dari 100 bisa didapatkan dengan perkalian 100×99×98× … ×3×2×1. Hasil yang tepat tidak akan bisa dihitung dengan kalkulator saintifik yang ada di pasaran. Untuk menghitungnya, kita perlu menggunakan perangkat lunak di komputer yang bisa melakukan penghitungan analitik seperti Mathematica (berbayar), Maxima (gratis), dan semacamnya. Dengan menggunakan Maxima, kita bisa melihat hasilnya adalah
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000.
Apabila menggunakan kalkulator saintifik untuk bisa mendapatkan hasil yang tepat seperti di atas, kita membutuhkan kalkulator yang bisa menampilkan 158 digit angka. Karena itu, penulis berani berspekulasi bahwa tidak ada kalkulator di pasaran yang bisa menampilkan hasil yang tepat. Akan tetapi, apabila kalkulator Anda cukup canggih, maka Anda akan mendapatkan nilai
9,3326 × 10157.
Bagaimana kalkulator saintifik Anda bisa mendapatkan nilai ini? Apakah dia mengalikan 100×99×98× … ×3×2×1? Jika Anda penasaran, silakan dicoba melakukan perkalian ini, sebelum Anda selesai, mungin kalkulator Anda akan memunculkan error. Kalau tidak, coba lihat nilai 1000! (seribu faktorial).
Memperkirakan nilai faktorial dari bilangan yang besar adalah salah satu objek studi dari statistika. Untuk memperkirakan nilai dari N!, kita bisa mengamati nilai logaritma naturalnya
ln N! = ln (N × (N – 1) × (N – 2) × … × 3 × 2 × 1)
= ln N + ln (N – 1) + ln (N – 2) + … + ln 3 + ln 2 + ln 1
Berapa jumlah dari logaritma ini? Grafik di bawah ini menunjukkan nilai ln(x) untuk x = 1 s.d. 100.
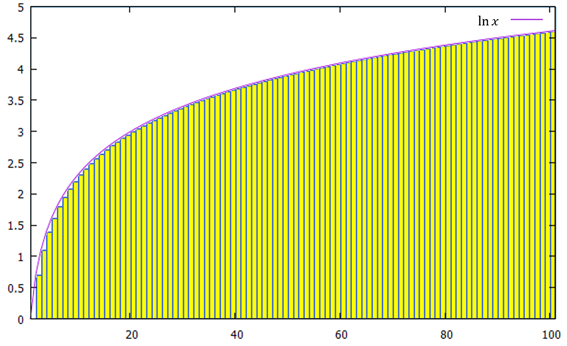
Nilai ln N!, yang merupakan luas area berwarna kuning, bisa diaproksimasi sebagai luas area di bawah kurva ln(x):
\ln N! \approx \int_0^N \ln x dx = N \ln N - N,
yang berarti aproksimasi N! \approx e^{N \ln N - N} = N^N e^{-N}. Mari kita bandingkan nilai ln N! dan N ln N – N untuk N = 100:
ln 100! = 363,74 dan 100 ln 100 – 100 = 360,52.
Perbedaan atau ketidakakuratan ini muncul dari aproksimasi integral yang kita lakukan.
Aproksimasi yang lebih tepat adalah aproksimasi Stirling,
N! \approx N^N e^{-N} \sqrt{2\pi N}
atau
\ln 100! \approx 100 \ln 100 - 100 + \ln \sqrt{200\pi} = 363,74
sehingga
100! \approx 9,33 \times 10^{157}.
Aproksimasi inilah yang umum digunakan untuk menghitung faktorial dari bilangan yang besar.
Bahan bacaan:
- Boas, M. L. (2006). Special Functions. In Mathematical methods in the physical sciences. John Wiley & Sons.
Penulis:
Adam Badra Cahaya, Dosen di Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Indonesia.
Kontak: adam(at)sci.ui.ac.id
