Ketika kita mempelajari matematika, kita bisa menemukan nama Archimedes, seorang matematikawan Yunani yang sangat brilian pada masanya. Tokoh yang satu ini lahir di Syracuse dan hidup sekitar tahun 287-212 SM. Konon, Archimedes juga merupakan otak di balik rancangan persenjataan bagi tentara Syracuse, yaitu ketika Perang Punic II antara Kartago melawan Romawi sedang berlangsung, dan pada saat itu Syracuse berada di pihak Kartago. Dikisahkan bahwa kemudian Archimedes dibunuh oleh tentara Romawi saat berkutat dengan pekerjaan geometrinya.
Kali ini kita akan membahas cara berpikir Archimedes yang sangat brilian dalam memperkirakan nilai pi (π). Sejak di bangku SD, guru-guru telah memperkenalkan bilangan ini ketika membahas lingkaran. Rumus yang sangat monumental tentu saja rumus keliling lingkaran, yaitu dua π dikalikan dengan jari-jari lingkaran. Keliling lingkaran bisa juga dinyatakan sebagai hasil kali π dengan diameter (garis tengah) lingkaran,
KO = πD,
π = KO/D,
dengan KO adalah keliling lingkaran dan D adalah diameter lingkaran.
Dari rumus ini terlihat bahwa π tidak lain adalah perbandingan (rasio) antara keliling dan diameter lingkaran. Telah umum diketahui bahwa nilai π seringkali didekati dengan angka 3,14 ataupun 22/7. Perlu diingat bahwa angka-angka tersebut hanya pendekatan, karena π adalah bilangan irasional.
Ada hal lainnya yang perlu untuk diketahui, yaitu Archimedes maupun orang-orang pada masa itu tidak menyebut perbandingan keliling dan diameter lingkaran sebagai π karena penggunaan simbol π dengan nilai 3,14… digunakan di kemudian hari oleh Leonhard Euler (1707 – 1793), tepatnya pada tahun 1736. Sebelum masa Archimedes, orang-orang telah mengetahui bahwa keliling lingkaran adalah sekitar 3 kali dari diameternya, tetapi angka 3 tersebut adalah perkiraan yang kasar sekali.
Sekitar tahun 250 SM, Archimedes memulai petualangan matematisnya mencari nilai π. Archimedes mendapati bahwa pada poligon beraturan (segi banyak yang panjang sisi-sisinya sama), semakin banyak sisi yang dimiliki oleh poligon tersebut, bentuknya semakin menyerupai lingkaran.
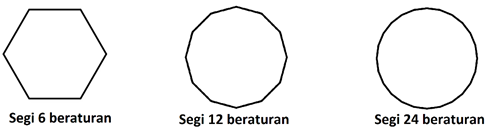
Jika sebuah poligon beraturan dipadankan dengan sebuah lingkaran dengan panjang jari-jari lingkaran tersebut sama dengan panjang “jari-jari” poligon, nilai keliling poligon semakin mendekati nilai keliling lingkaran saat jumlah sisi poligon diperbanyak. Dengan kata lain, jika jumlah sisi poligon menuju tak berhingga, nilai kelilingnya semakin menuju nilai keliling lingkaran. Dalam bahasa matematika, kita dapat menyatakan:
limn→ꝏ Kn = KO,
dengan n adalah jumlah sisi poligon beraturan dan Kn adalah keliling poligon beraturan bersisi n. Berdasarkan konsep ini, π sebagai rasio keliling dan diameter lingkaran dapat dinyatakan sebagai
π = KO/D = limn→ꝏ Kn/D.
Masalah berikutnya adalah nilai keliling poligon beraturan yang kita hitung pasti selalu lebih kecil daripada nilai keliling lingkaran, karena jika poligon dan lingkaran tersebut kita tumpuk, pasti poligon selalu berada di dalam lingkaran. Hal yang dilakukan Archimedes adalah membuat poligon beraturan lainnya, yaitu poligon yang terletak di luar lingkaran, namun sisi-sisinya tetap menyinggung lingkaran, atau dengan kata lain, kini lingkaranlah yang berada di dalam poligon tersebut, kebalikan dari jenis poligon yang pertama. Karena terletak di luar lingkaran, maka keliling poligon jenis kedua selalu lebih besar daripada poligon jenis pertama. Jadi, terdapat dua jenis poligon pada metode perhitungan Archimedes ini, yaitu poligon di dalam lingkaran (disebut sebagai inscribed polygon), dan poligon di luar lingkaran (disebut sebagai circumscribed polygon).
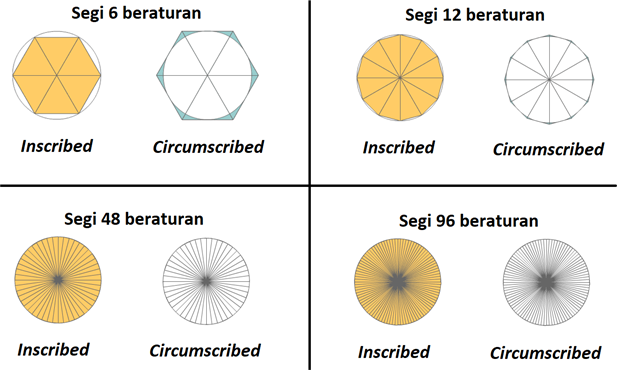
Dari ilustrasi inscribed polygons dan circumscribed polygons, menjadi lebih jelas terlihat bahwa semakin banyak sisi pada inscribed polygons, ukuran poligon menjadi semakin besar (dengan jari-jarinya dipertahankan konstan), sedangkan semakin banyak sisi pada circumscribed polygons, ukuran poligon menjadi semakin kecil (dengan sisi-sisi poligon dipertahankan menyinggung lingkaran). Jadi, persamaan π = limn→ꝏ Kn/D kini berlaku umum, baik bagi inscribed polygons dan circumscribed polygons.
Inti dari poin ini disadari oleh Archimedes. Namun, alih-alih mencari nilai eksak dari π, ia justru memperkirakan rentang tempat nilai π berada. Archimedes menggunakan inscribed polygon dan circumscribed polygon yang sama-sama bersisi 96. Jika melirik kembali ilustrasi inscribed polygons dan circumscribed polygons, kita dapat menerima bahwa penggunaan poligon bersisi 96 sudah cukup baik untuk pendekatan bentuk lingkaran. Pada inscribed polygon, Archimedes mendapati rasio antara keliling poligon dan diameter lingkaran adalah 3 10/71 (dalam bentuk pecahan desimal dapat didekati dengan angka 3,1408) , sedangkan pada circumscribed polygon, rasio antara keliling poligon dan diameter lingkaran adalah 3 1/7 (dalam bentuk pecahan desimal dapat didekati dengan angka 3,1429). Jadi, nilai π berada pada rentang kedua angka tersebut, ia lebih besar daripada 3 10/71, dan lebih kecil daripada 3 1/7.
Nilai π (yang telah kita ketahui saat ini) dengan hanya mengambil 4 angka di belakang koma adalah 3,1416. Oleh karena itu, rentang nilai π yang didapatkan Archimedes sudah benar, dan bisa kita katakan bahwa metodenya sangat brilian, terlebih jika kita mengingat bahwa hal itu dilakukan sekitar tahun 250 SM. Selain itu, rentang nilai π ala Archimedes yang relatif sangat kecil itu juga sudah sangat baik untuk kepentingan praktis.
Hal menarik lainnya adalah kita dapat menapaktilasi metode Archimedes ini. Dengan berbekal kemampuan trigonometri dan kalkulator (yang tentu saja dapat digunakan untuk melakukan perhitungan trigonometri), kita dapat menghitung rasio keliling poligon dan diameter lingkaran, dengan jumlah sisi poligon yang lebih banyak: sisi 100, sisi 1.000, bahkan sisi 10900 pun bisa kita hitung jika kita mau.
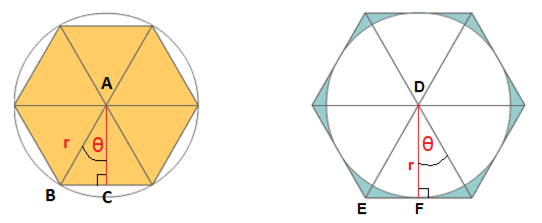
Dari ilustrasi analisis geometri pada inscribed polygon dan circumscribed polygon, terlihat bahwa panjang satu buah sisi inscribed polygon adalah dua kali BC. Kita bisa tuliskan:
sin θ = BC/AB,
BC = AB sin θ = r sin θ,
dengan r adalah jari-jari lingkaran (sekaligus jari-jari inscribed polygon). Panjang satu sisi inscribed polygon adalah 2 dikalikan dengan r sin θ. Rumus ini dapat diperumum untuk inscribed polygon bersisi n, sehingga kelilingnya adalah
Kn = 2 n r sin θ.
Sementara itu, pada circumscribed polygon, terlihat bahwa panjang satu buah sisi circumscribed polygon adalah dua kali EF.
tan θ = EF/DF,
EF = DF tan θ = r tan θ,
dengan r adalah jari-jari lingkaran. Panjang satu sisi circumscribed polygon adalah 2 r sin θ. Rumus ini dapat diperumum untuk circumscribed polygon bersisi n, sehingga kelilingnya adalah
Kn = 2 n r tan θ.
Pada poligon beraturan bersisi 96, nilai θ (dalam derajat) adalah (360° : 96)/2 = 1,875°. Dengan memasukkan angka ini, untuk lingkaran berdiameter 1 satuan (memiliki jari-jari ½ satuan), dapat kita peroleh rasio antara keliling inscribed polygon dengan diameter lingkaran adalah 3,1410, sedangkan rasio antara keliling circumscribed polygon dengan diameter lingkaran adalah 3,1427. Jadi, angka-angka untuk rentang nilai π yang diperoleh Archimedes sebenarnya sangat dekat dengan hasil perhitungan menggunakan rumus trigonometri kita.
Poin penting dari pembahasan ini adalah bagaimana Archimedes berpikir out of the box dibandingkan dengan orang-orang di sekitarnya. Terkadang pengembaraan pikiran ketika kita berhadapan dengan permasalahan matematis dapat membawa kita kepada solusi yang cantik dan elegan. Jadi, ketika menemukan suatu permasalahan matematis, lebih baik untuk tidak malas berpikir, bukan?
Bahan bacaan/tontonan:
- Lie Yuen Ming, Seri Tokoh Dunia 52: Archimedes, Elex Media Komputindo (2008).
- https://en.wikipedia.org/wiki/Pi
- Saluran YouTube “Rolando Asisten” https://www.youtube.com/watch?v=PU-oKCAZNNI
- https://www.pbs.org/wgbh/nova/archimedes/pi-nf.html
Penulis:
Muhammad Lawrence Pattersons, Mahasiswa S-2 Ilmu Fisika, Universitas Indonesia.
Kontak: muhammad4lawrence(at)gmail(dot)com



