“Mengapa makanan segar biasanya disimpan dalam lemari pendingin?” Jawabannya, tentu agar makanan dapat bertahan dan dikonsumsi dalam jangka waktu lebih lama karena pada suhu rendah bakteri pembusukan makanan berkembang biak dengan laju lebih lambat dibandingkan pada suhu kamar. Dari jawaban ini beberapa pertanyaan yang lebih mendalam dapat diutarakan, “Jika mula-mula terdapat sejumlah bakteri, dapatkah kita memprediksi jumlah bakteri dalam selang waktu tertentu? Apakah pertumbuhan bakteri mengikuti suatu persamaan matematika sederhana?”
Secara umum, terdapat beberapa model matematika untuk memprediksi pertumbuhan populasi makhluk hidup. Di sini, kita akan menerapkan teknik matematika sederhana pada mikrobiologi untuk membuat model pertumbuhan bakteri, khususnya pertumbuhan bakteri Listeria monocytogenes yang umum ditemui di lingkungan sekitar.
Model primer dan sekunder pertumbuhan bakteri
Model pertumbuhan bakteri dapat dihitung dengan pendekatan matematika sederhana karena beberapa alasan. Dua alasan paling utama adalah: (1) bakteri berkembang biak secara aseksual, yakni membelah diri, sehingga beberapa faktor reproduktif yang berlaku pada organisme tingkat tinggi (misalnya, persaingan dan peluang keberhasilan kawin) dapat diabaikan, dan (2) laju pertumbuhan bakteri secara kasar hanya merupakan fungsi dari beberapa kondisi fisis tempat bakteri tumbuh, seperti suhu, kadar garam, keasaman (pH) dan kelembapan.
Dalam model primer, pertumbuhan bakteri di suatu tempat pada waktu t hanya bergantung pada jumlah bakteri x(t). Model primer paling sederhana dikenal dengan model Malthusian, yang dapat dinyatakan dengan persamaan diferensial,
\displaystyle \frac{dx(t)}{dt} = \mu x(t) \ldots (1)
dengan \mu \geq 0 adalah suatu konstanta. Persamaan di atas berarti laju pertumbuhan bakteri sebanding dengan jumlah bakteri saat itu.
Solusi persamaan (1) adalah
x(t) = x_0 e^{\mu t}
dengan x_0 adalah jumlah bakteri pada kondisi awal, yakni ketika t = 0, sehingga x \rightarrow \infty ketika t \rightarrow \infty dan \mu \rightarrow 0. Ini kurang realistis karena pada waktu tertentu pertumbuhan bakteri seharusnya berhenti seiring nutrisi yang berkurang dan habis pada tempat bakteri tumbuh. Oleh karena itu, disarankan bahwa µ merupakan suatu fungsi dari jumlah bakteri dan dapat dinyatakan sebagai
\mu = \mu_{\textrm{max}} u(x) \ldots(2)
dengan \mu \geq 0 merupakan besaran yang mengatur laju pertumbuhan bakteri dan u(x) adalah fungsi variabel tunggal.
Menurut model logistik, u(x) dapat dinyatakan sebagai
u(x) = 1 - \displaystyle \frac{x}{x_{\textrm{max}}} \ldots(3)
dengan xmax adalah jumlah maksimum bakteri yang dapat hidup pada suatu sampel, misalnya sepotong keju. Jadi, ketika x = xmax, kita peroleh µ = 0 dan persamaan (1) menjadi dx/dt = 0. Artinya, pertumbuhan bakteri menjadi stagnan (berhenti).
Nilai x biasanya dinyatakan dalam satuan cfu/cm2. cfu merupakan singkatan dari colony forming unit, yakni jumlah sel bakteri yang mampu untuk membelah diri pada keadaan tertentu. Penyelesaian model logistik dinyatakan oleh
x = \displaystyle \frac{x_{\textrm{max}}}{1 + \left(\frac{x_{\textrm{max}}}{x_0} - 1\right)e^{-\mu_{\textrm{max}} t}} \ldots(4)
Pada model sekunder, µmax merupakan fungsi lingkungan, contohnya suhu dan keasaman (pH). Pada kesempatan kali ini, kita hanya akan membahas efek suhu pada pertumbuhan bakteri. Salah satu model yang banyak digunakan adalah model Ratkowsky yang dimodifikasi dan dinyatakan oleh persamaan berikut:
\mu_{\textrm{max}} = A^2 (T - T_{\textrm{min}})^2 [1 - e^{B (T - T_{\textrm{max}})}] \ldots(5)
dengan Tmin dan Tmax adalah suhu minimum dan maksimum bakteri dapat hidup dan membelah diri, sedangkan dan adalah konstanta riil yang nilainya disesuaikan dengan pengamatan. Nilai-nilai µmax, Tmin, Tmax, A, dan B bergantung pada spesies bakteri.
Sebelum membahas lebih lanjut, perlu diketahui bahwa fungsi-fungsi pada persamaan (3) dan (5) bersifat fenomenologis, artinya fungsi-fungsi tersebut tidak diturunkan dari teori-teori yang lebih mendasar, tetapi dipilih sedemikian rupa untuk menjelaskan hasil pengamatan. Parameter bertahan hidup bakteri Listeria monocytogenes akan dibahas sebagai berikut.
Listeria monocytogenes
L. monocytogenes adalah bakteri yang banyak ditemui pada makanan, misalnya keju dan daging. Jumlah minimum bakteri yang dibutuhkan dalam tubuh manusia sehingga gejala infeksi muncul itu tergolong cukup rendah, yakni ~1000 sel. Infeksi bakteri ini dapat menyebabkan keguguran janin. Bakteri L. monocytogenes mampu bertahan hidup (namun tidak membelah diri) pada suhu −18oC, dan membelah diri pada suhu −1,5oC hingga 45oC (Tmin = −1,5 oC, Tmax = 45 oC). Dalam lingkungan netral (pH = 7,0), bakteri ini tumbuh paling cepat pada suhu 37oC dan rentang kadar garam 12-16%.
Banyak penelitian telah dilakukan untuk memprediksi pertumbuhan L. monocytogenes. Menurut penelitian yang dilakukan oleh Augustin dan Carlier, didapatkan nilai µmax sekitar 0,8/jam pada suhu 30oC dan pH = 7,0.
Memprediksi jumlah bakteri sebagai fungsi waktu dan suhu
Dari beberapa sumber, kita telah mengetahui beberapa faktor pertumbuhan L. monocytogenes, antara lain µmax, Tmin, dan Tmax,. Namun, untuk memprediksi jumlah bakteri sebagai fungsi waktu dan suhu, kita perlu mencari konstanta-konstanta A > 0 dan B > 0 pada µmax.
Dalam kalkulus, turunan pertama suatu fungsi kontinu adalah nol pada titik maksimum dan minimum. Seperti yang sudah dijelaskan, pertumbuhan L. monocytogenes maksimum adalah pada suhu T = 37oC. Dengan demikian, µmax memenuhi persamaan
\displaystyle\left(\frac{\partial \mu_{\textrm{max}}}{\partial T}\right)_{T = 37^\circ \textrm{C}} = 0 \ldots(6)
Substitusi persamaan (5) ke dalam persamaan (6) menghasilkan
\displaystyle\Big( 2A^2 (T - T _{\textrm{min}}) [1 - e^{B (T - T_{\textrm{max}})}] - A^2 B (T - T _{\textrm{min}})^2 e^{B(T - T_{\textrm{max}})} \Big)_{T = 37^\circ \textrm{C}}= 0 \ldots(7)
Penyederhanaan persamaan (7) menghasilkan
(T - T _{\textrm{min}}) B + 2 = 2 e^{-B (T - T_{\textrm{max}})} \ldots(8)
Substitusi Tmin = −1,5 oC, Tmax = 45 oC, dan T = 37 oC, kita peroleh
38,5 B + 2 = 2e^{8B} \ldots(9)
Di sini, kita untuk sementara mengabaikan satuan oC untuk menyederhanakan penulisan. Persamaan (9) merupakan persamaan transendental sehingga persamaan tersebut tidak dapat diselesaikan secara aljabar. Untuk menyelesaikan persamaan (9) digunakan metode sebagai berikut: fungsi-fungsi pada ruas kiri dan kanan diplot secara terpisah, titik potong kedua fungsi tersebut (B > 0) adalah solusi yang dicari, sebagaimana ditampilkan pada gambar.
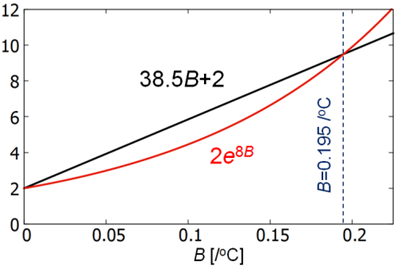
Dari gambar di atas, dapat disimpulkan bahwa solusi persamaan (9) adalah B = 0,195/ oC Untuk menentukan nilai A, kita gunakan data eksperimen bahwa µmax bernilai sekitar 0,8/jam pada suhu 30oC. Dengan menggunakan nilai-nilai tersebut, A dapat dihitung berdasarkan persamaan (5):
A = \displaystyle \frac{\sqrt{0,8/\textrm{jam}}}{31,5^\circ \textrm{C}} [1 - e^{(0,195\times -15)}]^{-1/2} = 0,029\textrm{jam}^{-1/2}~^\circ \textrm{C}^{-1} \ldots (10)
Setelah menentukan nilai A dan B, maka µmax untuk L. monocytogenes bisa digambarkan sebagai fungsi suhu T.

Dari gambar di atas, dapat disimpulkan bahwa laju pertumbuhan L. monocytogenes perlahan-lahan meningkat dengan naiknya suhu hingga T = 37 oC, kemudian turun secara drastis hingga T = 45 oC ketika bakteri ini mati.
Dengan menggabungkan hasil ini dengan persamaan (4), kita dapat memprediksi populasi L. monocytogenes (variabel x) sebagai fungsi waktu t pada 24 jam pertama sejak bakteri tumbuh dan rentang suhu -1,5^\circ \textrm{C} \leq T \leq 45^\circ\textrm{C}. Di sini kita memisalkan bahwa mula-mula terdapat 500 bakteri per cm2 (x0 = 500 cfu/cm2) dan membatasi jumlah bakteri yang dapat tumbuh hingga 10000 sel per cm2 (xmax = 10000 cfu/cm2). Fungsi x(t, T) kemudian dapat dinyatakan dalam gambar berwarna.
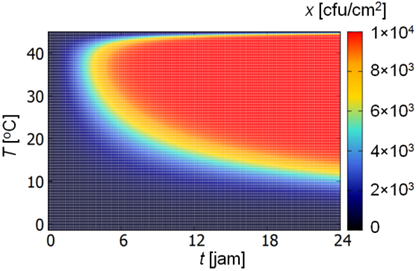
Agar lebih mudah dimengerti, mari kita plot x sebagai fungsi waktu t pada beberapa temperatur (T = 5; 15; 25; 37; 42 oC) yang ditunjukkan pada gambar di bawah ini. Kita bisa lihat kurva yang menunjukkan pertumbuhan populasi bakteri berbentuk huruf ‘S’, yang dikenal dengan kurva sigmoid.
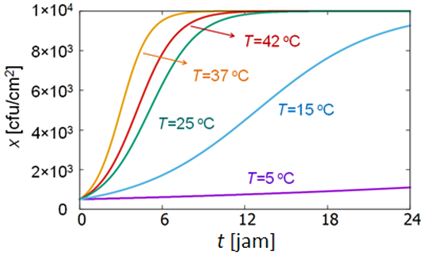
Kurva sigmoid menunjukkan fase pertumbuhan bakteri sejak proses pembelahan diri berlangsung. Pada beberapa jam pertama bakteri tumbuh secara eksponensial. Kemudian, pertumbuhan bakteri melambat seiring peningkatan populasi bakteri secara linear (mengikuti persamaan garis). Terakhir, terjadi fase stagnan, yakni proses pembelahan diri berhenti dan jumlah bakteri tetap. Dari gambar di atas, pertumbuhan populasi bakteri berlangsung paling pesat pada suhu T = 37 oC. Pada kondisi itu, µmax untuk L. monocytogenes bernilai maksimum sebagaimana yang telah dibahas.
Kita secara singkat telah membahas model logistik yang diterapkan pada pertumbuhan L. monocytogenes. Model dan metode matematika yang digunakan dapat diterapkan pada spesies bakteri lain. Model tersebut tentu hanya merupakan pendekatan karena kondisi nyata pertumbuhan bakteri jauh lebih rumit dan melibatkan banyak faktor. Namun, kita telah melihat bagaimana matematika mampu memprediksi dan memberikan gambaran sekilas mengenai proses pertumbuhan makhluk hidup sederhana.
Bahan bacaan:
- Baranyi, Modelling and parameter estimation of bacterial growth with distributed lag time, PhD Thesis, University of Szeged (2010).
- S. Schvartzman dkk., Frontiers in Cellular and Infection Microbiology 4, 90 (2014).
- H. Zwietering dkk., Applied and Environmental Microbiology 57, 1094-1101 (1991).
- Anonim, The control and management of Listeria monocytogenes contamination of food, Food Safety Authority of Ireland (2005).
- -C. Augustin & V. Carlier, International Journal of Food Microbiology 56, 29-51 (2000).
Penulis:
Fenda Rizky Pratama, Mahasiswa S-3 Jurusan Fisika di Tohoku University, Jepang.
Kontak: faustonhisdesk(at)yahoo(dot)com