Alkisah, Rusdi meletakkan koper besarnya di samping lemari kamar. Kamar itu masih bersih, sebersih apa yang bisa kita harapkan dari sebuah hotel bintang empat. Rusdi memandang seisi kamar, menelisik dengan teliti setiap detail ruang yang akan menjadi tempat tinggalnya di negeri Ginseng untuk beberapa hari ke depan. Saat itulah Rusdi memperhatikan pemandangan di balik jendela.
Langit mulai gelap. Matahari tentulah sudah terbenam beberapa waktu lalu. Rusdi segera beranjak ke kamar mandi, mengambil air wudu, dan bersiap melaksanakan salat Maghrib. Secara refleks, Rusdi menghadapkan diri ke arah kiblat, yaitu arah barat daya. Atau, setidaknya begitulah hasil pemikiran Rusdi setelah melihat peta dunia menjelang berangkat, tadi pagi.
Sayangnya, Rusdi tak yakin. Ia memutuskan membuka aplikasi penunjuk arah kiblat di ponselnya, yang dengan sigap menunjukkan arah kiblat untuk kota tempatnya tinggal. Panah yang bergoyang di balik layar ponsel itu menunjukkan satu arah. Arah yang membuat Rusdi bingung.
“Barat laut? Eh kok?”
Menandingi Bapak Geometri
Geometri, bagi sebagian dari kita, termasuk ke dalam daftar panjang materi yang diakrabi dengan setengah hati sepanjang tahun-tahun di jenjang pendidikan. Waktu-waktu mempelajari geometri menjadi saat ketika sederetan rumus menjemukan yang biasa bersemayam di buku matematika digantikan oleh berbagai gambar aneka bentuk. Gambar-gambar tersebut mungkin sekilas terlihat sebagai sebuah penyegaran, sampai kita memergoki ada lagi deretan rumus yang menemani semuanya.
Ya, geometri mungkin terdengar mengerikan bagi sebagian kita. Tetapi, mungkin yang lebih mengerikan adalah orang yang menyatukan konsep dasar-dasar semua bangun di sekitar kita dalam satu kesatuan. Di bagian selanjutnya, kesatuan sejenis itu akan disebut konsep geometri.

Publikasi ilmiah dalam bidang geometri sudah ada sejak abad keenam sebelum Masehi, di saat figur-figur cendekiawan Yunani Kuno seperti Thales mendalami perhitungan panjang, luas atau volume berbagai bentuk bangun datar atau ruang. Meski demikian, geometri masih terbatas pada pengunaan praktis sehari-hari hingga abad ketiga sebelum Masehi.
Di abad itu, seorang cendekiawan bernama Euklides memutuskan untuk menyusun sebuah konsep geometri “normal”, yaitu konsep geomeri yang biasa kita kenal, dengan beberapa gagasan dasar, atau aksioma. Dengan menyatakan aksioma-aksioma tersebut, Euklides menunjukkan bahwa konsep geometri, beserta bermacam ciri khas dari bangun-bangun yang terbentuk di dalamnya, dapat disatukan dalam satu kerangka logika sederhana.
Aksioma-aksioma (atau gagasan-gagasan dasar) yang digunakan Euklides dalam mendasari konsep geometri “normal” adalah sebagai berikut:
- Setiap dua titik sembarang dapat dihubungkan oleh satu garis lurus.
- Setiap garis lurus sembarang dapat diperpanjang sampai panjang tak hingga.
- Setiap garis lurus sembarang dapat mewakili jari-jari dari sebuah lingkaran, dengan salah satu ujung garis menjadi titik pusat.
- Setiap sudut siku-siku memiliki besar yang sama, 90°.
- Jika dua buah garis sembarang memotong sebuah garis lain pada sudut yang berbeda, perpanjangan kedua garis itu akan berpotongan.
Aksioma yang diperkenalkan Euklides ini kemudian menjadi gagasan dasar bagi konsep geometri “normal” yang senantiasa kita pakai sehari-hari. Berhubung saat itu orang belum mengenali tipe konsep geometri yang lain, maka penisbatan nama Euklides bagi konsep geometri terkait tidak diperlukan. Artinya, ketika orang-orang di zaman Romawi dulu membicarakan geometri, yang mereka maksud pastilah konsep geometri Euklides. Lagipula, bagi mereka saat itu, hanya konsep geometri Euklides-lah yang bisa mereka bayangkan.
Menjelajahi Muka Bola
Semua berubah ketika orang mulai mendalami dunia pelayaran di Masa Penjelajahan. Pengetahuan akan bentuk Bumi yang (relatif) bulat telah cukup diterima oleh berbagai kalangan. Peta-peta untuk navigasi para pelaut mulai dikembangkan dalam usaha meratakan lengkung muka Bumi menjadi bidang datar yang dapat dicitrakan pada selembar kertas.
Pada saat itulah, orang mulai mendapati adanya perbedaan antara proyeksi pada peta dengan kenyataan sebenarnya, yang berakar pada kelengkungan muka Bumi. Alhasil, metode paling baik untuk menerapkan ilmu navigasi di muka Bumi adalah dengan memperlakukan permukaan Bumi secara apa adanya. Dengan kata lain, menerapkan ilmu navigasi pada permukaan sebuah bola.
Kendala pertama dalam menyusun dasar-dasar navigasi dengan permukaan bola adalah adanya aksioma dari konsep geometri Euklides yang tidak berlaku pada permukaan bola. Pada permukaan sebuah bola, panjang suatu tarikan garis terbatas, bergantung pada ukuran bola tempatnya berada. Dua tarikan garis yang memotong satu tarikan garis lain dengan sudut yang sama, ketika digambarkan pada permukaan bola, ternyata bisa berpotongan ketika berada di permukaan sebuah bola. Padahal, pada konsep geometri Euklides, seharusnya kedua garis terkait tidak berpotongan.
Berdasarkan hal-hal tersebut, konsep geometri pada permukaan bola kemudian perlu dibedakan dengan konsep geometri Euklides. Maka, kita sekarang mengenal konsep geometri bola. Inilah salah satu contoh dari konsep geometri non-Euklides, yang baru dikenal para matematikawan sejak abad ke-17.
Seperti apa konsep geometri bola ini?
Sebagaimana tersirat di penjabaran sebelumnya, konsep geometri bola berkutat dengan bangun bola, khususnya di permukaan bola. Pada konsep geometri bola, ‘titik’ didefinisikan sebagaimana biasa, tetapi ‘garis’ tidak cocok lagi digunakan, mengingat permukaan bola yang melengkung. Analogi bagi ‘garis’ pada geometri bola adalah busur, yang didefinisikan sebagai jarak tempuh terdekat antara dua titik di permukaan bola (juga dikenal dengan istilah busur geodesik) atau garis geodesik.
Jika kita cukup iseng untuk meneruskan perjalanan busur baru tersebut, ia akan terus memanjang mengelilingi bola, hingga kembali menemui titik asalnya. Hasilnya adalah sebuah lingkaran, yang membagi bola menjadi dua bagian dengan ukuran tepat sama besar. Lingkaran ini kemudian dinamai lingkaran besar karena lingkaran tersebut adalah lingkaran yang paling besar yang mungkin dibentuk pada permukaan sebuah bola.
Ketika hanya sepotong dari lingkaran itu yang kita tinjau, potongan itu disebut busur lingkaran besar. Pada hakikatnya, setiap busur, sesuai definisinya pada konsep geometri bola, merupakan busur lingkaran besar. Setiap lingkaran besar memiliki dua titik yang posisinya paling jauh dari lingkaran terkait, kedua titik ini disebut kutub. Sebagai contoh, jika kita membicarakan garis khatulistiwa Bumi sebagai lingkaran besar, kedua kutub yang dimaksud di sini adalah kutub utara dan kutub selatan geografis Bumi.
Berbedanya geometri bola dengan geometri Euklides menyebabkan perlunya menyusun rumusan-rumusan baru dalam melakukan perhitungan pada permukaan bola. Perhitungan yang paling umum digunakan dengan memanfaatkan sebuah bangun bernama segitiga bola. Segitiga bola hampir sama dengan segitiga “normal”, dalam pengertian ia terdiri dari tiga titik sudut dan tiga busur yang menghubungkan ketiga titik. Beda antara keduanya, sebagaimana tersirat dari namanya, segitiga bola terletak di permukaan bola.
Mengapa yang dipilih segitiga? Karena segitiga adalah bangun dua dimensi yang paling sederhana, sehingga mudah dimanfaatkan dalam perhitungan. Perhitungan yang jamak dipakai sendiri disebut trigonometri bola, yang pada dasarnya hanya berbeda dengan trigomonetri “normal” pada jenis geometri tempat ia diterapkan.
Sampai saat ini, terkait geometri bola dan segitiga bola, ada beberapa informasi yang telah didapat. Informasi tersebut adalah:
- Pengertian segitiga bola adalah bangun yang terbentuk dari tiga busur.
- Setiap busur pada permukaan bola adalah busur lingkaran besar.
- Busur lingkaran besar adalah potongan dari sebuah lingkaran besar.
Ketiga informasi ini dapat digabungkan menjadi definisi segitiga bola yang singkat dan padat (meski belum tentu jelas) sebagai berikut:
“Segitiga bola adalah bangun pada permukaan bola yang terbentuk dari perpotongan tiga lingkaran besar.”
Definisi ini secara tak langsung menyiratkan bahwa setiap busur yang menghubungkan dua dari tiga titik sudut segitiga bola adalah busur geodesik.
Beranjak dari pemahaman ini, mungkin ada yang merasa sudah siap untuk memanfaatkan segitiga bola, terutama mereka yang telah memiliki dasar yang baik dalam mempelajari geometri Euklides. Sayangnya, tetap saja, geometri bola adalah geometri non-Euklides sehingga berbagai macam rumusan yang biasa kita pakai ketika memainkan bangun di geometri Euklides tidak serta-merta dapat digunakan pada geometri bola.
Misalkan segitiga bola yang telah dibahas sebelumnya diambil sebagai contoh. Jika seseorang menggambar segitiga menurut konsep geometri Euklides, segitiga yang ia dapat adalah segitiga ‘datar’ Namun, jika seseorang menggambar segitiga pada permukaan bola, segitiga yang ia dapat adalah segitiga yang ‘melengkung’.
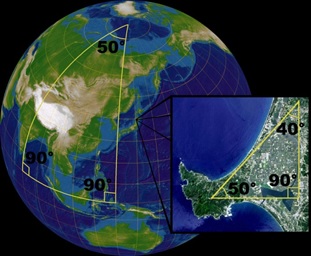
Perbedaan kelengkungan ini kemudian membawa kita kepada salah satu pembeda utama antara segitiga ‘normal’ dengan segitiga bola: Jumlah besar ketiga sudut segitiga bola lebih besar dari 180°.
Makin melengkung sebuah segitiga bola, atau makin luas ia menutupi permukaan bola, makin besar pula jumlah besar sudutnya, menjauhi 180° hingga nilai maksimum besar sudut sebesar 540°. Begitu pula sebaliknya, semakin mendatar segitiga bola yang dimaksud, ia akan menutupi luas yang lebih kecil, dan jumlah sudutnya pun akan semakin dekat dengan 180°.
Dalam perhitungan di dunia nyata, sebuah segitiga bola bahkan mungkin saja menjadi cukup kecil sehingga ia secara praktis menjadi sebuah segitiga Euklidean, alias ‘datar’. Tak jauh beda dengan manusia yang cenderung memahami permukaan Bumi sebagai hamparan tanah datar, akibat ukuran Bumi yang demikian besar ketika dibandingkan dengan manusia.
Geometri Bola Buat Apa
Baiklah, kita sudah diperkenalkan dengan sebuah konsep geometri yang relatif baru, konsep geometri bola, beserta sedikit penjelasan tentang bangun segitiga bola. Tak pelak, sebagian dari kita mungkin akan bertanya-tanya, geometri bola buat apa?
Kegunaan konsep geometri bola, yang paling utama, tentunya adalah penerapannya pada permukaan sebuah bola. Pada bola-bola yang biasa kita temui dalam kehidupan sehari-hari, entah itu bola sepak, bola basket, atau bola tenis, seringkali kita tak memfokuskan perhatian hanya pada permukaannya (pengecualian mungkin perlu diberikan kepada ilmuwan dalam dunia olahraga yang harus mendesain bola sebaik mungkin supaya berfungsi dengan optimal).
Sebenarnya, hampir tak ada bola yang permukaannya diperhatikan sedemikian rupa sampai perlu dihitung-hitung menggunakan perhitungan geometri bola. Setidaknya hanya ada dua bola yang bernasib demikian: bola langit dan bola bumi. Kebanyakan dari para pembaca sekalian mungkin sudah familiar dengan bola bumi, baik Bumi sebagai benda langit berbentuk hampir bola, atau mungkin miniatur bola bumi di kelas yang kerap disebut globe. Tapi, bola langit? Apalagi ini?
Bola langit adalah salah satu sisa paham geosentris yang masih lestari dipakai hingga masa kini. Meskipun paham geosentris sendiri sudah lama padam sejak ditenggelamkan oleh Copernicus dkk dengan paham heliosentris, astronom masa kini masih mendapati bola langit sebagai salah satu konsep yang penting dalam pengamatan astronomi.
Konsep bola langit berawal dari pandangan orang zaman dahulu, yang menganggap bintang gemintang di langit selayaknya kilau hiasan langit malam. Bintang yang demikian banyak, namun tak terjangkau. Dari pemahaman akan tak terjangkaunya bintang, mungkin bisa saja kita berimajinasi bahwa mereka memutuskan untuk menganggap seluruh bintang di langit memiliki jarak yang sama dari mata individu yang sedang mengamati mereka.
Seluruh bintang ini kemudian bisa kita anggap “menempel” pada suatu “permukaan” yang jaraknya tak terhingga dari mata para pengamat. Ketika kita menyusun bintang-bintang yang terletak di sembarang arah pada jarak yang sama dari suatu titik, bangun ruang apakah yang akan didapati? Tentu saja bola. Ketika seisi langit yang kita lihat kemudian ditempelkan pada kulit bola, bentuk bola apa yang akan kita dapati? Dialah bola langit.
Dalam penerapannya, geometri bola pada bola langit dan bola bumi secara umum dapat dibilang serupa. Astronom menggunakan perhitungan geometri bola untuk memetakan posisi benda langit, baik bintang (termasuk Matahari), planet, komet, asteroid ataupun benda langit lainnya. Sebagaimana para kartograf (pembuat peta) akan bersemangat memetakan pulau atau kenampakan alam lain yang baru mereka temukan di peta, astronom akan senantiasa bersemangat memetakan objek yang mereka amati pada peta bintang.
Beberapa dari objek di langit malam, seperti planet, Bulan, dan Matahari, bergerak cukup cepat di bola langit, sehingga perubahan posisinya perlu diamati dengan seksama dari hari ke hari. Begitu pula mode transportasi yang menyusuri gelombang lautan dan gemulung awan, mereka membutuhkan panduan arah yang jelas supaya tak tersesat akibat tak adanya daratan sebagai acuan. Dalam memandu kendaraan (atau memata-matai planet) yang berkelana itulah, trigonometri bola mengambil peran mengantarkan para penumpang (atau astronom) hingga sampai ke tujuan.
Kemudian, perhitungan geometri bola dalam astronomi menjadi sangat berperan ketika seorang astronom ingin menghubungkan posisi suatu objek, katakanlah bintang, di langit malam, dengan posisi objek dari sudut pandang sang astronom. Trigonometri bola juga diperlukan ketika seseorang ingin mengarahkan dirinya pada lokasi yang ia inginkan. Misalnya, mencari arah kiblat untuk menunaikan salat.
Karena objek tata surya seperti Matahari, Bulan, maupun planet-planet, bergerak relatif cepat, perhitungan yang seksama dengan mengandalkan trigonometri bola akan sangat diperlukan dalam mengamati sebuah benda langit di waktu tertentu. Begitu pula seseorang yang hendak melaksanakan salat setelah menempuh perjalanan panjang, ia akan membutuhkan trigonometri bola (baik secara manual atau memanfaatkan aplikasi) untuk menentukan arah kiblat yang cukup akurat.
Kira-kira demikianlah kegunaan dari apa yang disebut geometri bola. Meskipun memang kurang familiar di khalayak ramai, sebenarnya geometri bola telah memegang peranan penting dalam kehidupan manusia saat ini. Semoga tulisan singkat ini bermanfaat untuk kita semua!
Bahan bacaan:
- http://en.wikipedia.org/wiki/Spherical_geometry
- http://en.wikipedia.org/wiki/Celestial_coordinate_system
Penulis:
Gianluigi Grimaldi Maliyar, alumnus Tohoku University, Jepang.
Kontak: gian.gmaliyar(at)gmail(dot)com.



