“Kalkulus adalah hasil perjuangan intelektual yang dramatis yang telah berlangsung selama 2500 tahun,” demikianlah ungkapan matematikawan Richard Courant mengenai kalkulus.
Kalkulus adalah studi mengenai limit. Operasi limit ini selanjutnya berkembang menjadi operasi diferensial (disebut pula turunan) dan integral. Operasi-operasi tersebut diperkenalkan dalam mata pelajaran matematika di SMA, sehingga pada hakikatnya kalkulus bukanlah hal yang asing bagi para pelajar yang telah menjelajahi rimba matematika yang berisi limit, diferensial, dan integral.
Selain kalkulus, vektor juga merupakan salah satu materi yang dipelajari dalam mata pelajaran matematika SMA, bahkan menjadi irisan mata pelajaran matematika dan fisika. Di antara pembahasan lanjutan mengenai vektor adalah medan vektor, yaitu entitas matematika yang didefinisikan oleh suatu fungsi vektor.
Fungsi vektor adalah suatu fungsi yang mengaitkan setiap titik pada suatu daerah di dalam suatu ruang dengan sebuah vektor. Berikut ini adalah contoh fungsi vektor:
\mathbf{V}(x,y,z) = 2xy^5 z \hat{i} + (8xyz+xz^2) \hat{j} - 7 yz^7 \hat{k}.
Variabel x, y, dan z menunjukkan bahwa \mathbf{V} adalah suatu fungsi, sedangkan \hat{i}, \hat{j}, dan \hat{k} merepresentasikan vektor-vektor satuan. Artinya, \mathbf{V} mengandung dua buah tanda pengenal, yaitu tanda pengenal yang menunjukkan bahwa ia adalah suatu fungsi dan tanda pengenal yang menunjukkan bahwa ia adalah vektor. Dengan demikian, \mathbf{V} adalah sebuah fungsi vektor yang mendefinisikan suatu medan vektor.
Sekarang kita akan mencoba menghitung besarnya medan vektor \mathbf{V} pada sembarang titik, misal pada titik (x,y,z)=(0,1,1):
\mathbf{V}(0,1,1) = 2(0)(1)^5(1)\hat{i} + [8(0)(1)(1) + (0)(1)^2]\hat{j} - 7(1)(1)^7 \hat{k} = -7 \hat{k}.Jadi, besarnya medan vektor \mathbf{V} di titik (0, 1, 1) adalah senilai 7 satuan, pada arah -\hat{k} yang menunjukkan arah sumbu-z negatif. Jika kita pernah mempelajari materi vektor di sekolah, perlu diingat kembali bahwa vektor memiliki nilai dan arah. Karena \mathbf{V} adalah suatu fungsi, tentunya nilai medan vektor di sembarang titik lain dapat dihitung.

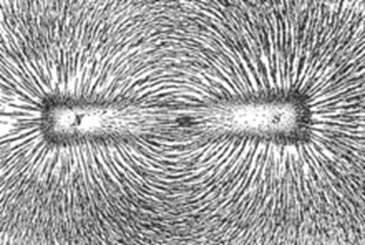
Jika masih terasa abstrak untuk dibayangkan, di alam kita bisa menemukan medan vektor, seperti medan listrik dan medan magnet. Ketika kita mengamati fenomena kemagnetan, sebenarnya kita sedang mengamati bentuk fisis dari sebuah medan vektor. Oleh sebab itu, materi pelajaran mengenai vektor juga masuk ke dalam mata pelajaran fisika mengingat banyak besaran fisika merupakan besaran vektor.
Dalam artikel ini, kita hendak memadukan kedua subjek penting dalam matematika ini, yaitu kalkulus dan vektor. Oleh karena itu, mari kita mengenal “kalkulus vektor” (atau “kalkulus medan vektor”). Perlu diketahui bahwa pembahasan mengenai kalkulus vektor sebenarnya cukup luas, dan apa yang ditulis di dalam artikel ini hanya berupa pengenalan, sehingga penulis tidak memasukkan semua materi kalkulus medan vektor di dalam artikel ini.
Salah satu tujuan penulisan artikel ini adalah agar para pembaca dari kalangan pelajar, khususnya pelajar SMA yang memiliki minat untuk melanjutkan studinya ke bidang MIPA ataupun teknik, dapat memperoleh gambaran awal mengenai apa yang dipelajari dalam mata kuliah kalkulus, khususnya pada bahasan kalkulus medan vektor. Materi ini bisa menjadi salah satu materi yang seru dan menyenangkan untuk dipelajari di level matematika universitas.
Sebelum melangkah lebih jauh, terlebih dahulu diperkenalkan operator diferensial parsial yang berlaku pada fungsi multivariabel (fungsi yang memiliki banyak variabel, sebagaimana fungsi V yang telah kita singgung sebelumnya). Jika pada operator diferensial biasanya kita menggunakan simbol d (semisal pada operasi diferensial y terhadap x, yakni dy/dx), pada diferensial parsial kita menggunakan simbol ∂ (dibaca “doh”).
Diferensial parsial hanya menghasilkan turunan terhadap satu buah variabel dari suatu fungsi multivariabel, contohnya:
\displaystyle\frac{\partial}{\partial x} (8x^2yz + xz^2) = 16 xyz + z^2.
Operasi diferensial parsial di atas adalah turunan terhadap x, sehingga yang diturunkan hanya variabel x. Angka maupun variabel selain x dianggap sebagai konstanta (bukan variabel). Contoh lainnya untuk diferensial parsial terhadap y:
\displaystyle\frac{\partial}{\partial y} (8x^2yz + xz^2) = 8x^2 z + 0 = 8x^2 z.
Di dalam kalkulus medan vektor, salah satu operator utamanya adalah ∇ (dibaca “del” atau “nabla”), yang di dalam koordinat kartesian (koordinat dengan sumbu x, y, dan z yang saling tegak lurus) direpresentasikan oleh
\mathbf{\nabla} = \displaystyle \hat{i} \frac{\partial}{\partial x} + \hat{j} \frac{\partial}{\partial y} + \hat{k}\frac{\partial}{\partial z}.
Ada 3 operasi matematis yang melibatkan del, yaitu gradien, divergensi, dan curl (rotasi). Gradien adalah turunan vektor dari suatu fungsi skalar. Jadi, selain fungsinya dapat berubah karena diturunkan, fungsi yang terkena operasi gradien juga berubah dari skalar menjadi vektor. Di antara ciri-ciri fungsi skalar adalah tidak memiliki vektor satuan, sehingga fungsi skalar tidak memiliki arah seperti yang dimiliki oleh fungsi vektor. Operasi gradien terhadap suatu fungsi skalar f dapat ditulis sebagai
\mathbf{\nabla}f = \displaystyle \left( \hat{i} \frac{\partial}{\partial x} + \hat{j} \frac{\partial}{\partial y} + \hat{k}\frac{\partial}{\partial z} \right) f = \displaystyle \frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial y} \hat{j} + \frac{\partial f}{\partial z} \hat{k}.
Sekarang kita akan mencoba menghitung gradien dari suatu fungsi skalar. Misal kita memiliki fungsi skalar f = 4xyz, gradiennya adalah
\frac{\partial(4xyz)}{\partial x} \hat{i} + \frac{\partial(4xyz)}{\partial y} \hat{j} + \frac{\partial(4xyz)}{\partial z} \hat{k} = 4yz \hat{i} + 4xz \hat{j} + 4xy \hat{k}.
Terlihat bahwa fungsi skalar f tidak memiliki vektor satuan, sedangkan hasil dari gradien f memiliki vektor satuan \hat{i}, \hat{j}, dan \hat{k}. Contoh aplikasi operasi gradien adalah perhitungan medan gaya sentral, yang besaran gayanya dapat dirumuskan sebagai berikut:
\mathbf{F} = -\mathbf{\nabla}E_P,
dengan F adalah vektor medan gaya sentral, dan EP adalah energi potensial yang berkaitan dengan gaya sentral tersebut. Energi potensial adalah sebuah fungsi skalar, sedangkan gaya sentral adalah sebuah fungsi vektor. Contoh gaya sentral yang terdapat di alam adalah gaya gravitasi dan gaya listrik statis.
Operator berikutnya adalah operator divergensi. Jika sebelumnya operator gradien mengubah fungsi skalar menjadi fungsi vektor, operator divergensi ini mengubah fungsi vektor menjadi fungsi skalar. Divergensi adalah dot product (perkalian titik) antara del dan suatu fungsi vektor. Dari materi vektor yang dipelajari di SMA, kita dapat mengetahui bahwa perkalian titik antara dua buah vektor akan menghasilkan sebuah skalar (hanya memiliki nilai tanpa arah).
Misalkan kita memiliki dua buah fungsi vektor sebagai berikut:
\mathbf{C}(x,y,z) = C_x (x,y,z) \hat{i} + C_y (x,y,z) \hat{j} + C_z (x,y,z) \hat{k}, \mathbf{D}(x,y,z) = D_x (x,y,z) \hat{i} + D_y (x,y,z) \hat{j} + D_z (x,y,z) \hat{k}.
Setiap komponen dari medan vektor C dan D, yaitu Cx, Dx, Cy, Dy, Cz, dan Dz adalah fungsi dengan variabel x, y, dan z. Pada perkalian titik, komponen i dikalikan dengan komponen i, komponen j dikalikan dengan komponen j, dan komponen k dikalikan dengan komponen k, lalu hasil perkalian masing-masing komponen dijumlahkan, sehingga hasil akhirnya adalah berupa skalar dan tidak memiliki vektor satuan lagi.
Perkalian titik antara C dan D dapat ditulis sebagai berikut:
\mathbf{C}\cdot\mathbf{D} = (C_x \hat{i} + C_y \hat{j} + C_z \hat{k}) \cdot (D_x \hat{i} + D_y \hat{j} + D_z \hat{k}) = C_x D_x + C_y D_y + C_z D_z.
Terlihat bahwa hasil dari perkalian titik di atas adalah suatu skalar, dapat diketahui dari ketiadaan vektor satuan pada hasil akhirnya. Dengan menggunakan cara yang sama, kini kita dapat menulis ekspresi matematis dari operasi divergensi.
Misalkan kita kenakan operasi divergensi terhadap fungsi vektor C, kita bisa tulis operasi tersebut sebagai berikut:
\mathbf{\nabla}\cdot\mathbf{C} = \displaystyle \left( \hat{i} \frac{\partial}{\partial x} + \hat{j} \frac{\partial}{\partial y} + \hat{k}\frac{\partial}{\partial z} \right) \cdot (C_x \hat{i} + C_y \hat{j} + C_z \hat{k}) = \displaystyle\frac{\partial C_x}{\partial x} + \frac{\partial C_y}{\partial y} + \frac{\partial C_z}{\partial z}.
Jika fungsi Cx, Cy, dan Cz diberikan, kita dapat menghitung divergensi dari C. Salah satu contoh aplikasi operasi divergensi adalah hubungan matematis antara medan listrik dengan kerapatan muatan listrik, yaitu
\mathbf{\nabla}\cdot\mathbf{E} = \displaystyle\frac{\rho}{\epsilon_0},
dengan E adalah medan listrik, ρ adalah kerapatan muatan listrik, dan ϵ0 adalah permitivitas ruang hampa.
Operasi terakhir yang akan kita bahas dalam artikel ini adalah operasi curl atau rotasi, yaitu turunan fungsi vektor yang menghasilkan fungsi vektor juga. Curl adalah perkalian silang (cross product) antara operator del dengan suatu fungsi vektor. Perkalian silang vektor dapat diselesaikan menggunakan aturan Sarrus, seperti saat menyelesaikan determinan matriks 3×3.
Misalkan kita memiliki dua buah fungsi vektor G(x, y, z) dan H(x, y, z):
\mathbf{G}(x,y,z) = G_x (x,y,z) \hat{i} + G_y (x,y,z) \hat{j} + G_z (x,y,z) \hat{k}, \mathbf{H}(x,y,z) = H_x (x,y,z) \hat{i} + H_y (x,y,z) \hat{j} + H_z (x,y,z) \hat{k}.
Perkalian silang antara G dan H dengan menggunakan aturan Sarrus dapat ditulis sebagai berikut:
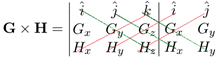
sehingga kita dapatkan:
\mathbf{G} \times \mathbf{H} = (G_y H_z - G_z H_y) \hat{i} + (G_z H_x - G_x H_z) \hat{j} + (G_x H_y - G_y H_x) \hat{k},
Dengan menggunakan cara yang sama, kita dapat menulis ekspresi matematis dari operasi curl.
Misalkan kita kenakan operasi curl terhadap fungsi vektor G, kita bisa tulis operasi tersebut sebagai berikut:
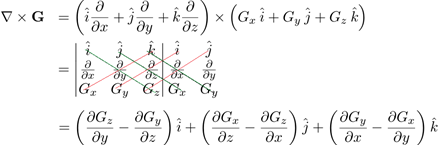
Jika fungsi Gx, Gy, dan Gz diberikan, kita dapat menghitung curl dari G dengan menggunakan rumus di atas. Salah satu aplikasi dari operasi curl dapat kita temukan pada hubungan matematis antara medan listrik dan medan magnet:
\mathbf{\nabla} \times \mathbf{E} = \displaystyle -\frac{\partial \mathbf{B}}{\partial t}.
dengan E adalah vektor medan listrik, dan ruas kanan menunjukkan nilai negatif dari diferensial parsial medan magnet (B) terhadap waktu (t). Turunan parsial tersebut merepresentasikan laju perubahan medan magnet terhadap waktu, dan juga merupakan vektor, sebagaimana medan magnet. Terlihat bahwa curl tetap menghasilkan vektor.
Demikianlah pengenalan kalkulus medan vektor. Sebagaimana yang disebutkan sebelumnya bahwa artikel ini hanya berupa pengenalan, tentunya banyak materi keren lainnya yang tidak tercakup di sini, seperti integral garis, integral permukaan, teorema divergensi Gauss, teorema Stokes, dan teorema Green pada bidang. Bagi para pembaca yang merasa tertarik dengan materi ini, alangkah baiknya untuk mencoba membuka-buka buku teks kalkulus dan memulai pengalaman bermatematika yang cukup menantang.
Last but not least, kata orang, sih, banyak berlatih soal-soal matematika merupakan salah satu jurus untuk meningkatkan kemampuan bermatematika. My exercise, my adventure!
Bahan bacaan:
- Dale Varberg, Edwin J. Purcell, Steven E. Rigdon, Calculus, Eighth Edition, Prentice Hall (2000).
- George B. Arfken, Hans J. Weber, Mathematical Methods for Physicists, Sixth Edition, Elsevier Academic Press (2005).
- https://en.wikipedia.org/wiki/Vector_field
Penulis:
Muhammad Lawrence Pattersons, Mahasiswa S-2 Ilmu Fisika, Universitas Indonesia.
Kontak: muhammad4lawrence(at)gmail(dot)com



