Pernahkah kita berpikir bagaimana struktur elektronik suatu sistem molekuler baik dalam kondisi tereksitasi maupun kondisi dasar (ground state)? Apakah mungkin teori-teori atau model matematis disusun sedemikian rupa guna menyatakan bagaimana “kondisi” elektron di dalam suatu senyawa molekul?
Tujuan untuk mengamati bagaimana struktur elektronik dapat berbeda antara kondisi tereksitasi dan kondisi dasar ternyata dapat dijawab sekaligus diterangkan menggunakan instrumen analisis bernama magnetic circular dichroism (MCD). Oleh Mack dan Stillman (2008), secara spesifik disebutkan bahwa dengan menggunakan MCD, yang pada dasarnya merupakan instrumen spektroskopi, momen angular orbital dan spin dapat dijabarkan.
MCD berlandaskan pada efek Faraday yang menggambarkan interaksi antara medan magnet dengan cahaya di dalam suatu medium. Ketika sebuah medan magnet tertentu diberikan secara sejajar pada sumbu lintasan cahaya, berkas sinarnya akan terpolarisasi akibat adanya perbedaan indeks refraksi. Perbedaannya adalah antara indeks refraksi medium untuk sinar terpolarisasi-kiri (lcp) dan sinar terpolarisasi-kanan (rcp). Dalam konteks ini, berkas sinar dimodelkan lewat secara sejajar pada sebuah bidang dan bidang itulah yang berotasi.
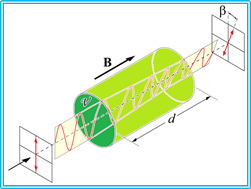
Dengan demikian, pengamatan MCD dilakukan sebagai implikasi adanya interaksi antara medan magnet luar dan elektron di keadaan dasar maupun tereksitasi. Interaksi tersebut mengakibatkan timbulnya perbedaan molekul menyerap berkas sinar terpolarisasi (Holmquist, 1986). Akan tetapi, apa yang membedakan antara MCD dengan instrumen nuclear magnetic resonance (NMR) mengingat keduanya menggunakan medan magnet? Jawabannya ialah MCD tidak berbasis pada resonansi spin seperti NMR, tetapi berbasis pada serapan sinar terpolarisasi yang bergantung panjang gelombangnya.
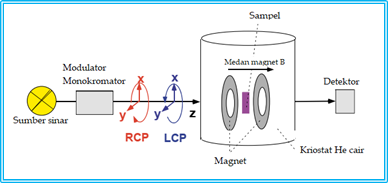
Nah, bagaimana spektra dari MCD dapat diprediksikan secara teoretis? Mau tak mau, suka atau tak suka, tinjauan lewat mekanika kuantum adalah penjabaran yang digunakan dalam hal tersebut. Kita tidak akan menjabarkan detail perumusannya di sini, tetapi pada dasarnya spektrum optis dapat direpesentasikan sebagai solusi dari persamaan gelombang Schrödinger. Spektrum tersebut merupakan indikasi dari energi transisi dan kuat osilator dari momen dipol transisi antara dua keadaan kuantum yang berbeda.
Parameter paling signifikan yang perlu diperhitungkan adalah momen dipol elektron (m). Hal ini disebabkan oleh fakta bahwa di dalam spektroskopi rentang ultraviolet hingga cahaya tampak yang memerikan keadaan dasar serta keadaan tereksitasi elektron di dalam sistem molekuler, parameter m memiliki nilai kurang-lebih 5 kali lebih besar daripada momen dipol magnetik (μ).
Baik serapan (absorption) maupun pancaran (emission) foton dengan panjang gelombang tertentu akan menghasilkan sebaran ulang (redistribution) muatan dalam molekul berdasarkan pada keadaan dasar elektron maupun tereksitasinya. Secara khusus untuk kasus senyawa enansiomer, yaitu senyawa dengan struktur molekul yang tak dapat diimpitkan dengan citra bayangan cerminnya, diketahui bahwa senyawa tersebut dapat menyerap sinar dengan polarisasi lcp maupun rcp bergantung pada redistribusi elektron secara heliks.
Ketika kita meninjau suatu molekul yang dikenai medan magnet, kita harus merujuk pada efek Zeeman, suatu fenomena fisika yang diteliti dan ditemukan oleh Pieter Zeeman yang mengantarnya memperoleh penghargaan Nobel Fisika pada tahun 1902. Dia menemukan fakta ilmiah bahwa dengan adanya medan magnet eksternal, garis-garis spektra akan terpecah menjadi beberapa komponen.
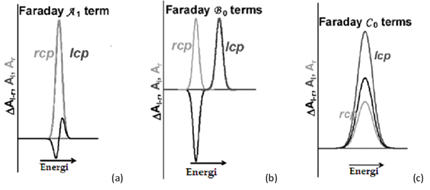
Di dalam analisis dengan MCD, terdapat besaran-besaran yang menjadi perhatian, yang disebut Faraday terms, yaitu \mathcal{A}_1, \mathcal{B}_0, dan C0. Masing-masing digunakan untuk (1) mendeskripsikan besarnya efek medan magnet pada pemecahan Zeeman dari serapan lcp dan rcp, (2) percampuran keadaan medan-nol (mixing of zero-field states) akibat medan magnet luar, dan (3) perubahan hunian keadaan dasar (ground state population adjustment) dari pemecahan Zeeman.
Transisi elektronik berdasarkan pada spektroskopi MCD dinyatakan dalam persamaan:
\frac{\Delta A_{l-r}}{E} = 152,5 Bcl \left[\mathcal{A}_1 \left(-\frac{df}{dE}\right) + \left(\mathcal{B}_0 + \frac{C_0}{k_B T}\right) \right] ,
dengan ΔAl–r ialah serapan diferensial antara lcp dan rcp, B adalah kuat medan magnet luar, cl ialah hasil kali antara konsentrasi sampel dengan panjang sampel, E menunjukkan energi (cm‑1), dan f adalah fungsi bentuk gelombang yang sudah dinormalisasi (umumnya berbentuk kurva Gaussian). Artikel ini tidak hendak menjabarkan terlalu terperinci mengenai analisis MCD, tetapi ada baiknya kita mengetahui makna setiap Faraday term di atas.
Faraday term pertama, \mathcal{A}_1, dipengaruhi oleh kombinasi momentum sudut orbital (L), momentum sudut spin (S), momen magnetik pada sumbu z (μz), matriks dipol elektrik terkait polarisasi lcp dan rcp, serta degenerasi keadaan tereksitasi dari sistem. Faraday term kedua, \mathcal{B}_0, terkait dengan transisi saat tiada percampuran antara keadaan dasar dan keadaan tereksitasi akibat induksi oleh medan magnet luar. Terakhir, Faraday term ketiga, C0, bergantung pada suhu sesuai rumusan C_0 \propto 1/k_B T, dengan kB ialah tetapan Boltzmann. Dengan demikian, dapat dibedakan dari dengan cara mengukur spektra pada suhu kamar dan suhu kriostat mengingat tidak bergantung pada suhu.
Nah, sekarang, bagaimana instrumen beserta analisis MCD digunakan di dalam penelitian? Pada tahun 2014, Habel-Rodriguez dkk. menggunakan analisis MCD untuk mengkaji struktur elektronik [Re2X4(PMe3)4]+ dengan X = Cl, Br.
Spektra yang diperoleh adalah spektra C-term, yang menunjukkan bahwa ada ketergantungan terhadap temperatur. Hasil analisis mereka dirangkum dalam tabel.
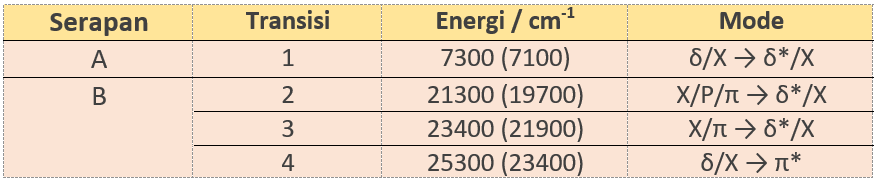
Di sini, δ → δ* merupakan transisi yang terkait langsung dengan interaksi Re–Re δ dan Re–L . Transisi 2 dan 3 menandai promosi satu elektron dari orbital ligan yang telah terisi menuju orbital δ* Re–Re, sedangkan transisi 4 diprediksi muncul karena promosi satu elektron dari orbital δ Re–Re menuju orbital virtual π* Re–Re.
Di penelitian lain oleh Kizaki dkk. pada tahun (2017), dilakukan spektroskopi MCD ftlaosianin double-decker dengan spesi Tb(III) di antara kedua ligan. Di dalam sistem tersebut, terdapat dua mode transisi yang diberi nama QL dan QH yang asalnya dari transisi elektronik HOMO (highest occupied molecular orbital) menuju LUMO (lowest unoccupied molecular orbital) di dalam ligan ftalosianin.
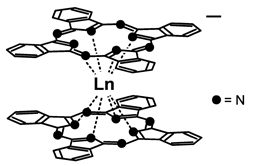
Penelitian ini dilakukan untuk mengkaji interaksi antara momentum sudut total J dari ligan dengan total angular momentum Tb(III) L. Interaksi tersebut dirangkum dalam dua notasi penting: Lz dan ΔJ-L dengan Lz adalah komponen L di sumbu z. Penelitian ini melaporkan untuk mode QL nilai Lz dan ΔJ-L masing-masing sebesar 2,3 ħ dan 1,4 cm-1 sedangkan untuk QH nilai Lz dan ΔJ-L dilaporkan sebesar 2,2 ħ dan 2,6 cm-1.
Meskipun analisis MCD ini tampak begitu “sakti”, kita harus mengerti pula bahwa ia tidak bisa berdiri sendiri. Para peneliti yang melibatkan kajian MCD sebenarnya juga menggunakan perhitungan kimia komputasi untuk menerangkan tingkatan energi elektron beserta struktur elektron itu sendiri. Mengapa? Sebab, transisi elektronik dari satu keadaan menuju keadaan yang lain tidak bisa diperkirakan dengan mudah.
Dengan banyaknya studi komprehensif seputar MCD, semoga dari pembaca ada yang dapat berkecimpung di dalamnya.
Bahan bacaan:
- Habel-Rodriguez, D.; Poineau, F.; Johnstone E.V.; Czerwinski, K.R.; Sattelberger, A.P.; Kirk, M.L. Chem. 2014, 53, 1260-1262.
- Kizaki, K.; Ozawa, H.; Kobayashi, T.; Matsuoka, R.; Sakaguchi, Y.; Fuyuhiro, A.; Fukuda, T.; Ishikawa, N. Commun. 2017, 53, 6168-6171.
- Mack, J.; Stillman, M.J.; Encyclopedia of Inorganic and Bioorganic Chemistry, 2011, John Wiley and Sons (DOI: 10.1002/9781119951438.eibc0289)
- Mack, J.; Stillman, M.J.; Kobayashi, N. Chem. Rev. 2007, 251, 429-453.
Penulis:
Langit Cahya Adi, Mahasiswa S-3 di Departemen Kimia, Osaka University.
Kontak: langit.cahyadi(at)gmail.com



