Matematika dan Kompresi Gambar Digital

Andi memiliki kamera digital single lens reflex (DSLR) model terbaru. Ia mengambil foto ikan mainan seperti pada gambar.

Contoh gambar mentah keluaran dari kamera DSLR.

Dalam format tidak terkompres (raw format), gambar ini memiliki tinggi 512 pixel dan lebar 768 pixel. Total pixel yang dibutuhkan adalah 512 x 768 = 393.216. Gambar digital disimpan ke dalam tiga kanal warna, yaitu merah, hijau, dan biru (RGB) sehingga total dibutuhkan 393.216 x 3 = 1.179.648 byte atau lebih dari 1 MB.

Jika Andi ingin mengunggah (upload) foto tersebut ke Facebook, secara otomatis server Facebook memperkecil ukuran foto untuk menghemat pemakaian harddisk pada server mereka dan untuk mempercepat komunikasi data. Metode kompresi JPEG (Joint Photographic Expert Group) merupakan salah satu contoh bentuk kompresi yang populer yang kita kenal. Dengan menggunakan kompresi JPEG, kita bisa memperoleh gambar dengan ukuran hanya 80 kB, atau hanya 7% dari kebutuhan memori pada raw format.

Contoh gambar terkompresi dalam format JPEG.

Dapatkah kalian menunjukkan perbedaan gambar pada raw format dan JPEG? Bagaimanakah prinsip kerja kompresi JPEG tersebut? Mari kita pelajari sekilas tentang ini.

Representasi basis dua

Gambar yang muncul di layar monitor komputer terbagi atas sejumlah pixel. Pixel adalah suatu blok terkecil yang menyusun gambar. Perhatikan gambar grayscale suatu rumah yang memiliki ukuran pixel baris 512 x kolom 768.

Gambar grayscale ini memiliki ukuran pixel baris 512 x kolom 768.

Untuk menghasilkan gambar tersebut, komputer mendeteksi tingkat kehitaman warna dengan skala 0 (hitam) – 255 (putih).

Jika kita perbesar gambar grayscale tersebut sampai batas maksimumnya, kita dapat melihat blok-blok pixel yang menyusun gambar.

Setiap warna pada blok pixel penyusun gambar merupakan hasil konversi dari angka-angka pada skala grayscale yang bernilai 0-255 seperti ditunjukkan tabel berikut ini.

150	154	160	157	106	140	147	142	141	147	132	150	171	117	136
144	159	125	121	157	143	132	136	153	138	155	164	169	162	152
190	175	169	155	161	136	152	158	141	162	147	153	161	168	169
185	203	139	161	151	159	145	167	179	167	150	155	165	159	158
151	153	163	152	160	152	164	131	131	51	124	152	154	145	143
164	162	158	167	157	164	166	139	132	138	119	148	154	139	146
147	148	143	155	169	160	152	161	159	143	138	163	132	152	146
66	129	163	165	163	161	154	157	167	162	174	153	156	151	156
162	173	172	161	158	158	159	167	171	169	164	159	158	159	162
163	164	161	155	155	158	161	167	171	168	162	162	163	164	166
167	167	165	163	160	160	164	166	169	168	164	163	165	167	170
172	171	170	170	166	163	166	170	169	168	167	165	163	163	160
173	172	170	169	166	163	167	169	170	170	170	165	160	157	148
167	168	165	173	173	172	167	170	170	171	171	169	162	163	162
200	198	189	196	191	188	163	168	172	177	177	186	180	180	188

Dalam pemrosesan data di komputer, angka-angka tersebut diubah ke dalam sistem bilangan basis dua (biner) dengan satuan yang disebut bit. Satu bit memiliki nilai antara satu atau nol. Satu byte adalah satu unit penyimpanan di komputer yang berisi 8 bit. Jika setiap bit dapat mengisi dua data, antara 0 atau 1, dalam 1 byte kita dapat menyimpan sebanyak 2⁸ = 256 nilai yang mungkin. Misalkan angka 125 dalam desimal dapat dituliskan ke dalam basis biner menjadi

125	= 64 + 32 + 16 + 8 + 4 + 1
	= 0 x 128 + 1 x 64 + 1 x 32 + 1 x 16 + 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1
	= 0 x 27 + 1 x 26 + 1 x 25 + 1 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20
	= 011111012

Kode Huffman dan Algoritma Huffman

Ide untuk mengompres data berasal dari David Huffman, yaitu dengan mengganti representasi biner berdasarkan frekuensi kemunculan. Misalkan kita ingin menyumpan data “sassafras”, bila kita simpan karakter dalam bentuk ASCII, representasi biner akan seperti pada tabel berikut.

Huruf	ASCII	Biner	Kemunculan	Frekuensi Relatif
s	115	01110011	4 kali	4/9
a	97	01100001	3 kali	1/3
f	102	01100110	1 kali	1/9
r	114	01110010	1 kali	1/9

Kata “sassafras” tersusun atas 9 karakter sehingga total kita membutuhkan 9 x 8= 72 bit memori. Kita dapat mengompres data tersebut sesuai dengan algoritma Huffman.

Urutkan karakter dari frekuensi relatif terkecil ke yang terbesar.

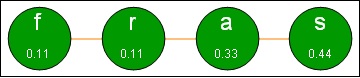
Dua karakter terendah, yaitu f dan r dijumlahkan, untuk membentuk parent baru, yang bernilai 0,22, dan membuat f dan r sebagai children.

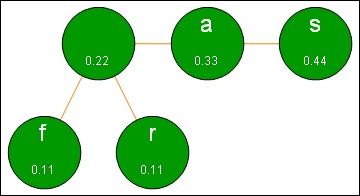
Mengulang langkah ke-2 untuk karakter a dan parent 0,22.

Mengulangi kembali langkah ke-3 untuk karakter s dan parent baru 0,55.

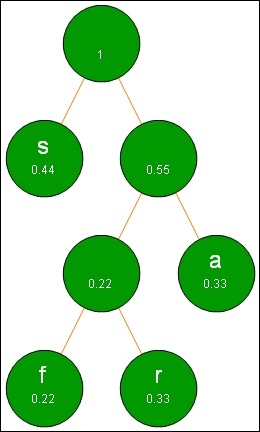
Memberi label 0 untuk cabang yang lebih kecil nilai frekuensi relatifnya dan 1 untuk cabang yang lebih besar nilainya.

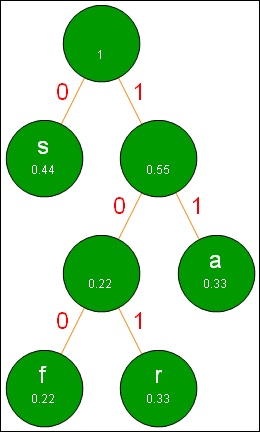
Setelah menerapkan algoritma Huffman, sekarang kita dapat menuliskan “sassafras” ke dalam kode Huffman.

Huruf	Biner	Huffman
s	01110011	0
a	01100001	11
f	01100110	100
r	01110010	101

Kode Huffman ini hanya membutuhkan 16 bit, atau kita telah menghemat lebih dari 75% memori.

Metode yang sama juga berlaku untuk kompresi data gambar digital. Kode Huffman ini hanyalah contoh sederhana bagaimana kita dapat menghemat alokasi memori yang kita pakai dalam penyimpanan data. Kompresi ini efisien jika variasi data tidak terlalu banyak. Jika teman-teman tertarik untuk melihat bagaimana kode Huffman dapat dipakai juga dalam kompresi data audio MP3, silakan baca juga artikel rubrik matematika majalah 1000guru edisi bulan Juni 2014.

Bahan bacaan:

http://www.whydomath.org/node/wavlets/imagecompression.html

Penulis:
Eddwi Hesky Hasdeo, mahasiswa doktor di Departemen Fisika, Tohoku University, Jepang.
Kontak: heskyzone(at)gmail(dot)com.

Matematika dan Kompresi Gambar Digital