Langit merupakan ruang luas yang terbentang di atas bumi. Sejak zaman kuno, langit selalu memberikan pertanyaan pada kita, bagaimanakah pergerakan dari bintang-bintang, planet-planet, matahari dan bulan? Karena penasaran dengan pertanyaan ini, bangsa Yunani dan India mengembangkan metode matematika dengan model geometri untuk mengetahui pergerakan benda-benda langit, yang kemudian disebut sebagai matematika astronomi. Ternyata, mereka menggunakan trigonometri untuk memecahkan pertanyaan besar ini sehingga akhirnya orang-orang kuno ini mengetahui posisi suatu planet di waktu tertentu.
Selanjutnya, bangsa Babilonia merupakan bangsa pertama yang mengamati pergerakan planet-planet (ada beberapa planet yang bisa diamati dengan mata telanjang: Merkurius, Venus, Mars, Jupiter dan Saturnus). Setelah mengamati selama bertahun-tahun, orang Babilonia menyadari bahwa semua planet tampaknya bergerak melewati jalur yang sama. Jalur ini disebut dengan ekliptika (ecliptic). Pengertian ekliptika yang lebih akurat didefinisikan sebagai jalur yang tampak yang dilalui terus-menerus oleh matahari atau planet-planet. Untuk lebih jelasnya, perhatikan gambar dengan contoh matahari.
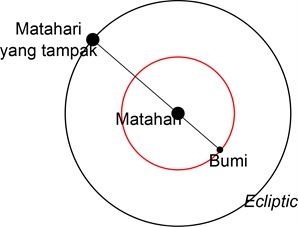
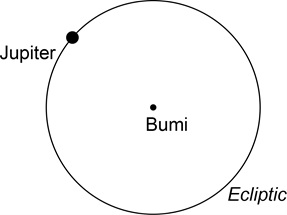
Letak matahari sebenarnya ada di tengah lingkaran merah.Namun, jika dilihat dari bumi, matahari terletak lebih jauh dan berada pada jalur ekliptika yang bisa manusia lihat dari bumi.Planet-planet juga berputar mengelilingi bumi di jalur ekliptika dan setiap planet memiliki waktu yang berbeda untuk menyelesaikan satu putaran penuh. Misalnya, diperlukan waktu satu tahun untuk Merkurius dan Venus menyelesaikan satu putaran, dan tiga puluh tahun untuk Saturnus. Perhatikan gambar jalur ekliptika untuk contoh Jupiter.
Ketika planet melalui jalur ekliptika, secara periodik planet tersebut akan melambat, berhenti dan berbalik arah. Gerakan berbalik arah ini disebut gerakan mundur atau gerak retrograde. Gerakan ini pun tidak luput dari pengamatan orang Babilonia kuno. Gerakan retrograde sangat diperlukan untuk perhitungan nanti.
Sebuah model pergerakan planet diusulkan oleh Apollonius, seorang ahli ilmu ukur Yunani, pada tiga abad sebelum masehi. Pada model Apollonius, planet-planet bergerak secara seragam di sekitar jalur epicycle, sementara pusat epicycle bergerak tidak beraturan di sekitar bumi pada lingkaran yang lebih besar, yaitu deferent.
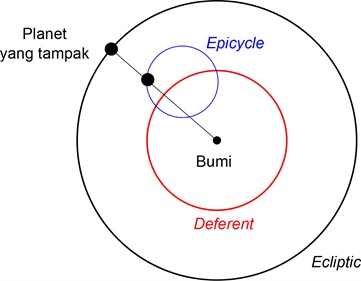
Waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh mengelilingi lingkaran (revolusi) disebut periode. Terdapat dua periode pada model Apollonius ini:
- Periode sideris
Periode ketika pusat epicycle mengelilingi deferent, atau waktu yang diperlukan planet (yang tampak) untuk kembali ke titik yang sama dari ekliptika.
- Periode sinodis
Periode ketika planet berevolusi terhadap epicycle, atau dapat diartikan sebagai waktu planet tersebut kembali ke titik awalnya
Model ini memiliki tiga parameter, yaitu r/R, T, dan S, dengan r adalah jari-jari epicycle, R jari-jari deferent, T periode sideris, dan S periode sinodis.
Dengan pengamatan yang cermat, bangsa Babilonia akhirnya menemukan pendekatan revolusi dari periode sideris dan sinodis. Sebagai contoh, mereka mengamati bahwa planet Mars menyelesaikan satu periode sideris nyaris dua tahun, sedangkan untuk periode sinodis diselesaikan selama dua tahun lebih sedikit. Data planet yang lengkap dapat diamati pada Tabel 1.
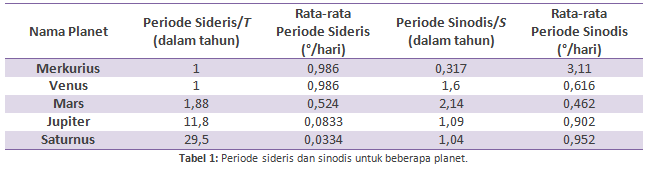
Selain mengamati periode planet-planet, para astronom kuno juga mengobservasi jarak dan waktu planet tersebut ketika mengalami gerakan retrograde. Hasilnya ditunjukkan pada Tabel 2.
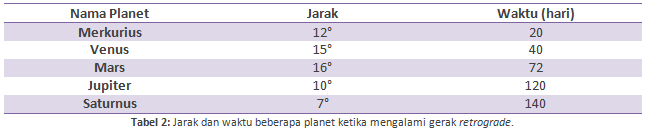
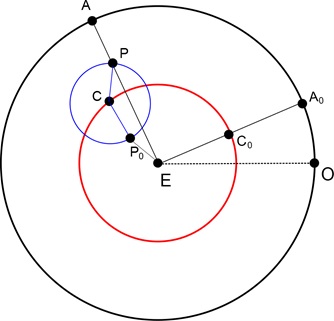
Sebelum kita dapat mencari posisi suatu planet, kita harus mencari rasio r/R terlebih dahulu. Rasio ini mendefinisikan panjang dari busur gerakan retrograde. Untuk menghitung r/R menggunakan Tabel 2, kita mulai pada saat epicycle, planet, dan bumi berada pada garis lurus, dengan planet Pdi titik P0 pada epicycle, seperti pada gambar berikut ini.
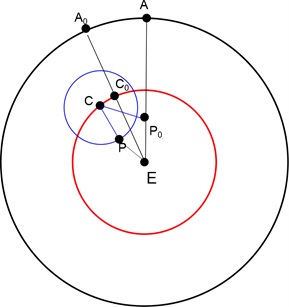
Pada gambar di atas, C0 adalah pusat epicycle saat ini dan A0 adalah lokasi planet yang tampak pada ecliptic. Titik C merepresentasikan pusat epicycle yang baru, titik A juga merupakan lokasi baru dari planet yang tampak. Jika r adalah sisi CP dan R adalah sisi EC dari segitiga ECP, berarti kita harus mengetahui setiap sudut di segitiga ECP untuk menemukan rasio EC/PC. Sekarang kita akan menghitung nilai r/R dari Planet Mars. Dalam perhitungan tersebut peran trigonometri tentu tidak terhindarkan.
Contoh: Planet Mars
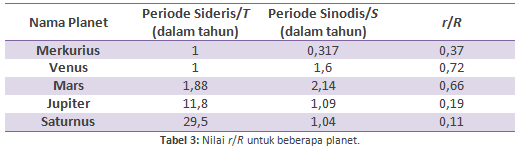
Berdasarkan data pada Tabel 2, nilai busur retrograde adalah (1/2)panjang = 8° (bernilai setengahnya karena planet bergerak secara seragam pada epicycle) dan (1/2)waktu = 36 hari (bernilai setengahnya karena pusat epicycle bergerak secara seragam pada deferent).
Berdasarkan data pada Tabel 1, rata-rata periode sinodis planet Mars adalah 0,462°/hari dan rata-rata periode sideris adalah 0,524°/hari. Dengan demikian,
Sudut ECP = busur P0P = rata-rata periode sinodis× (1/2)waktu = 16,6°
Sudut C0EC = busur C0C = rata-rata periode sideris × (1/2)waktu = 18,9°
Sudut A0EP = busur A0A = (1/2)panjang = 8°
Sudut PEC = sudut C0EC + sudut A0EP = 18.9° + 8° = 26,9°
Sudut CPE = 180° – (sudut PEC + sudut ECP) = 180° – (26,9° + 16,6°) = 136,5°
Dengan aturan sinus, r/R = CP/EC = sin(PEC)/sin(CPE) = 0,66.
Untuk planet-planet yang lain, hasilnya dapat dilihat pada Tabel 3.
Setelah kita menemukan parameter-parameter yang dibutuhkan, sekarang kita dapat mencari posisi dari planet tersebut. Perhitungan posisi ini melibatkan segitiga CEP yang telah kita hitung pada saat mencari r/R. Untuk lebih jelas, dapat dilihat modelnya seperti di bawah ini.
Untuk mencari posisi planet pada waktu T adalah dengan mengetahui panjang busur A0A kemudian dijumlahkan dengan sudut bujur saat T0 atau saat planet mengalami busur tengah A0O. Titik O adalah titik asal diukur saat waktu siang sama dengan waktu malam di suatu belahan bumi (equinox). Untuk mencari posisi planet saat T dibutuhkan sudut PEC. Sekali lagi kita ambil planet Mars sebagai contoh.
Misalkanpergerakan planet Mars terhadap busur retrograde telah diamati dengan alat-alat astronomi, dan diketahui bahwa busur tengah terjadi pada bujur 40°. Dengan data ini, kita akan menghitung posisi planet Mars 250 hari kemudian (untuk memudahkan dimisalkan R = 1 dan r = r/R).
Berdasarkan Tabel 1, diketahui bahwa rata-rata periode sinodis planet Mars adalah 0,462°/hari dan rata-rata periode sideris adalah 0,524°/hari.
Posisi bujur saat T0 = 40° dan waktu yang dibutuhkan dari T0 ke T adalah 250 hari.
Pada T, busur C0C = rata-rata periode sideris × waktu yang dibutuhkan = 0,524 × 250 = 131°
Busur P0P = rata-rata periode sinodis × waktu yang dibutuhkan = 0,462 × 250 = 115,5°
Sudut ECP = busur P0P = 115,5°
EC = R = 1
CP = r = 0,66
Dengan menggunakan aturan cosinus, PE = [EC2 + CP2 – 2(EC)(CP)(cos(ECP))]1/2= 1,416.
Dengan menggunakan aturan sinus, sin(PEC) = [CP sin(ECP)]/PE = 0,421 sehingga sudut PEC = arcsin(0,421) = 25o.
Busur A0A = busur C0C – sudut PEC = 131° – 25°= 106°
Bujur T = bujur T0 + Busur A0A = 40° + 106° = 146°.
Dengan demikian, diketahui letak planet Mars 250 tahun kemudian ada pada bujur 146°. Silakan untuk planet yang lain dicoba sendiri, ya!
Sangat menarik,kan, aplikasi trigonometri di dunia astronomi ini. Walaupun tidak terlalu akurat, tetapi model ini cukup menjawab pertanyaan bangsa-bangsa kuno yang penasaran dengan langit. Semoga menjawab pertanyaanmu juga.
Bahan bacaan:
Penulis:
Reyna Marsya Quita, mahasiswi master di Jurusan Matematika, Universitas Brawijaya.
Kontak: reynaquita2905(at)gmail(dot)com.