Pernahkah teman-teman menjumpai bujur sangkar ajaib yang berisi bilangan dengan penjumlahan baris, kolom dan diagonalnya bernilai sama? Contohnya adalah bujur sangkar berikut:
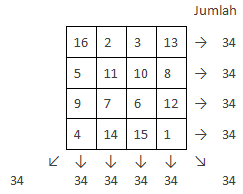
Perhatikan bahwa penjumlahan baris, kolom dan diagonal pada bujur sangkar di atas bernilai 34. Keren, bukan? Mau tahu bagaimana cara menyusunnya bahkan untuk sisi bujur sangkar 5 × 5 atau 10 × 10? Kita perlu mempelajari untai Thue-Morse. Dengan mempelajari untai Thue-Morse, hal-hal yang lebih menakjubkan tentang bilangan akan kalian saksikan sebentar lagi.
Untai Thue-Morse diperkenalkan secara implisit oleh ilmuwan Eugene Prouhet pada tahun 1851 dalam artikelnya tentang teori bilangan. Saat itu, Prouhet belum memberikan nama khusus untuk untai tersebut. Setelah itu, pada tahun 1906 Axel Thue membahas untai tersebut dalam penelitiannya tentang kombinatorika untai. Pada tahun 1921 Marston Morse menggunakannya untuk memecahkan masalah geometri diferensial. Setelah itu, untai tersebut dikenal dengan nama untai Thue-Morse, atau untai Prouhet-Thue-Morse.
Saat ini, studi tentang untai Thue-Morse telah banyak dihasilkan oleh para peneliti. Karena memuat nama “Morse”, kamu mungkin bertanya apakah untai Thue-Morse berkaitan dengan kode Morse. Jawabannya adalah tidak berkaitan, karena masing-masing “Morse” di sini merujuk kepada dua orang yang berbeda. Kode Morse digunakan dalam kode teks untuk berkirim pesan dengan alat yang disebut telegraf, yang ditemukan oleh Samuel F.B Morse pada tahun 1830-an.
Apakah untai Thue-Morse itu? Untai Thue-Morse adalah untai biner yang dibentuk secara iteratif (berulang) sebagai penyambungan antara prefiks dengan komplemen binernya dan prefiks pada iterasi awalnya adalah 0. Perlu diketahui bahwa komplemen biner dari 0 adalah 1, dan komplemen biner dari 1 adalah 0.
Iterasi pembentukan untai Thue-Morse diilustrasikan sebagai berikut:
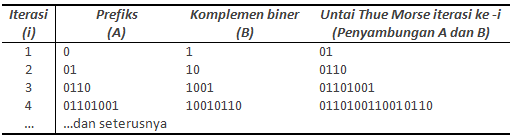
Jika tabel di atas dilanjutkan, untai Thue-Morse pada iterasi ke-6 memiliki panjang 64, yaitu: 0110100110010110100101100110100110010110011010010110100110010110.
Secara rumus, pembentukan untai Thue-Morse dinyatakan sebagai:
![]()
dengan U_k adalah untai Thue-Morse iterasi ke-k, \bar{U}_k adalah komplemen biner dari U_k, dan operator “o” adalah operasi penyambungan (concatenation) dua untai.
Untai Thue-Morse banyak digunakan dalam pemecahan berbagai masalah matematis. Dalam artikel ini dibahas dua di antaranya, yaitu permasalahan Prouhet-Tarry-Escott (“Prouhet-Tarry-Escott problem”) dan pembentukan bujur sangkar ajaib.
1. Permasalahan Prouhet-Tarry-Escott
Permasalahan Prouhet-Tarry-Escott dinyatakan sebagai berikut:
Diberikan sebuah bilangan bulat m > 1 dan sebuah r = 2n > m, tentukanlah dua himpunan saling lepas A = {a1, …, ar} dan B = {b1, …, br} sehingga berlaku:
a1k + a2k + … + ark = b1k + b2k + … + brk, untuk nilai k = 1, …, m.
Rumus di atas bermakna “penjumlahan pangkat k dari semua anggota A adalah sama dengan penjumlahan pangkat k dari semua anggota B”. Untai Thue-Morse dapat digunakan untuk menyelesaikan permasalahan Prouhet-Tarry-Escott dengan nilai m = 2, sebagaimana diilustrasikan berikut ini. Catatan: Untuk m > 2, penyelesaian dapat ditemukan dengan Generalized Thue-Morse, yang tidak dibahas dalam artikel ini.
Salah satu pemecahan dari permasalahan Prouhet-Tarry-Escott untuk m = 2 adalah:
r = 4, A = {1, 4, 6, 7}, dan B = {2, 3, 5, 8}
Bagaimana penjelasan tentang pemecahan tersebut? Ingat bahwa nilai k adalah 1 sampai m. Karena m = 2, nilai k adalah 1 atau 2. Nilai r adalah 4, yang berarti masing-masing himpunan A dan B beranggotakan 4 elemen. Perhatikan bahwa untuk k = 1, berlaku:
11 + 41 + 61 + 71 = 21 + 31 + 51 + 81
Demikian pula untuk k = 2, berlaku:
12 + 42 + 62 + 72 = 22 + 32 + 52 + 82
Dengan demikian r = 4, A = {1, 4, 6, 7}, dan B = {2, 3, 5, 8} adalah salah satu pemecahan dari permasalahan Prouhet-Tarry-Escott untuk m = 2.
Bagaimana cara menemukan pemecahan tersebut? Dengan bantuan untai Thue-Morse! Jika kita tetapkan r = 4, himpunan A dan B masing-masing memiliki 4 elemen. Oleh karena A dan B himpunan yang saling lepas dan irisannya adalah himpunan kosong, terdapat 8 elemen yang berbeda, yaitu 1, 2, …, 8. Pemilihan elemen-elemen yang masuk ke himpnan A dan B ditentukan berdasarkan untai Thue-Morse dengan panjang 8, yaitu 01101001. Caranya, pertama-tama tulislah elemen himpunan dan untai Thue-Morse sejara berjajar, seperti berikut ini:
![]()
Elemen yang berpadanan dengan 0 pada untai Thue-Morse menjadi anggota himpunan A, sedangkan yang berpadanan dengan 1 menjadi anggota himpunan B. Dengan demikian, diperoleh anggota himpunan A adalah 1, 4, 6, 7 dan anggota himpunan B adalah 2, 3, 5, 8. Mudah, bukan?
Sekarang, dengan cara serupa, cobalah kamu tentukan elemen-elemen untuk himpunan A dan B untuk r = 8 (r harus berbentuk 2n, dalam hal ini n = 3). Gunakan untai Thue-Morse panjang 16, yaitu 0110100110010110, dan elemen himpunannya adalah 1, 2, …, 16. Setelah itu periksalah hasilnya dengan rumus di atas; apakah penjumlahan pangkat k dari semua anggota A adalah sama dengan penjumlahan pangkat k dari semua anggota B, untuk k = 1 dan k = 2, sebagaimana ditunjukkan pada contoh sebelumnya. Kamu akan mendapatkan bahwa untuk masing masing nilai k, penjumlahan pada ruas kiri dan pada ruas kanan adalah sama!
2. Pembentukan Bujur Sangkar Ajaib
Bujur sangkar ajaib berukuran n × n berisi bilangan-bilangan yang jika dijumlahkan secara mendatar, menurun, maupun diagonal menghasilkan jumlah yang sama. Berikut adalah salah satu bujur sangkar ajaib berukuran 4 × 4.
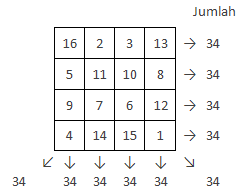
Yang menjadi pertanyaaan adalah: bagaimanakah cara menempatkan bilangan 1 sampai 16 ke dalam kotak-kotak kecil itu sehingga jika dijumlah secara mendatar, secara menurun, maupun secara diagonal memberikan hasil yang sama?
Kita dapat menggunakan bantuan untai Thue-Morse. Caranya, pertama-tama jajarkanlah bilangan 1 sampai 16 dan untai Thue-Morse panjang 16 sebagaimana berikut ini:
![]()
Setelah itu, isilah kotak-kotak kecil pada bujur sangkar berukuran 4 × 4 yang kosong dengan elemen yang berpadanan dengan 1 pada untai Thue-Morse, yaitu 2, 3, 5, 8, 9, 12, 14, dan 15. Pengisian sesuai urutan kotak, sehingga diperoleh bujur sangkar berikut ini:
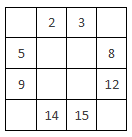
Selanjutnya, isilah kotak-kotak tersisa yang masih kosong dengan elemen yang berpadanan dengan 0 pada untai Thue-Morse, namun dalam urutan menurun yaitu 16, 13, 11, 10, 7, 6, 4, 1. Pada akhirnya kita peroleh bujur sangkar ajaib berikut ini:
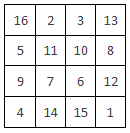
Mudah bukan? Metode ini dapat diterapkan untuk membentuk bujur sangkar ajaib berukuran 2n × 2n. Dengan cara tersebut, silakan teman-teman coba buat bujur sangkar ajaib berukuran 8 × 8. Gunakan prefiks untai Thue-Morse panjang 64. Untuk memudahkan, periksalah hasil penjumlahan setiap baris, setiap kolom dan juga setiap diagonalnya dengan bantuan kalkulator. Kamu akan mendapatkan bahwa jumlah bilangan pada semua arah tersebut sama! Selamat mencoba!
Bahan bacaan:
- https://en.wikipedia.org/wiki/Thue-Morse_sequence
- http://mathworld.wolfram.com/Thue-MorseSequence.html
- https://en.wikipedia.org/wiki/Prouhet-Tarry-Escott_problem
- https://www.jstor.org/stable/2321011
Penulis:
Ahmad Sabri, alumnus S-3 informatika dari Université de Bourgogne, Perancis. Staf pengajar di Universitas Gunadarma, Jakarta. Kontak: sabri(at)staff.gunadarma.ac.id, Situs web: http://sabri.staff.gunadarma.ac.id/



