Dalam pelajaran matematika, kita akrab dengan istilah “dimensi” yang secara kasar memberikan skala ukuran suatu bentuk geometris. Misalnya, dimensi nol terkait dengan titik, dimensi satu terkait dengan garis, dimensi dua terkait dengan permukaan atau bidang, dan dimensi tiga terkait dengan ruang. Namun, pernahkah teman-teman terbayang ada suatu benda berdimensi pecahan? Ternyata ada, namanya adalah fraktal.
Menurut kamus Webster, fraktal didefinisikan sebagai potongan yang tidak rata, salah satu variasi kurva yang tidak beraturan dan mengulangi dirinya sendiri pada skala tertentu. Konsep fraktal diusulkan oleh Mandelbrot, yang memberi istilah tersebut dari kata sifat bahasa latin yaitu fractus. Kata kerja yang berhubungan dengan fractus adalah frangere, yaitu memecah-mecah, membuat menjadi bagian-bagian yang tidak beraturan. Akan tetapi, di balik bentuk tak beraturan fraktal ini ada keteraturan dalam bentuk “kemiripan diri” (self-similarity), yaitu bentuk fraktal sebenarnya berasal dari suatu bentuk dasar yang teratur.

Menghitung Dimensi Fraktal
Untuk memahami sifat kemiripan diri dari suatu fraktal, kita perlu tahu cara menghitung dimensi fraktal. Nah, sebelum menghitung dimensi fraktal, kita perhatikan dulu cara menghitung dimensi dari sebuah objek. Berikut ini ada tiga contoh:
- Seperti yang bisa kita lihat, garis di bawah ini dibagi menjadi 4 baris yang lebih kecil. Masing-masing garis mirip dengan garis aslinya, tetapi mereka semua berukuran ¼ skala. Ini adalah gagasan paling sederhana dari sifat kemiripan diri.
![]()
- Kotak di bawah juga dipecah-pecah menjadi kotak yang lebih kecil. Masing-masing kotak kecil berukuran ¼ dari ukuran semula sehingga dibutuhkan 16 kotak kecil untuk membangun kotak besar.
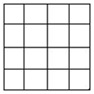
- Seperti halnya kotak di atas, kubus di bawah ini bisa dibagi-bagi menjadi kubus kecil yang mempunyai ukuran ¼ ukuran semula. Dibutuhkan 64 kubus kecil untuk membangun kubus besar.
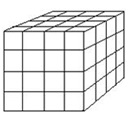
Dengan memperhatikan contoh-contoh tersebut, kita bisa melihat suatu pola:
$latex 4\ \ =\ 4^{1} \newline$
$latex 16\ =\ 4^{2} \newline$
$latex 64\ =\ 4^{3} \newline$
sehingga didapatkan persamaan:
$latex N\ =\ S^{D} \newline$
$latex N$ adalah jumlah pecahan kecil yang diperlukan untuk membuat bangun yang besar, $latex S$ adalah skala perbandingan antara bangun yang besar dibandingkan pecahan kecil, dan $latex D$ adalah dimensi. Sekarang kita memiliki alat untuk menghitung dimensi. Kita tinggal menghitung $latex D$ dalam persamaan di atas dengan menggunakan aturan logaritma:
$latex D\ =\displaystyle \frac{\log{N}}{\log{S}}$
Oke, sekarang kita ambil contoh sebuah fraktal untuk dihitung dimensinya. Fraktal ini bernama “kurva Koch”.
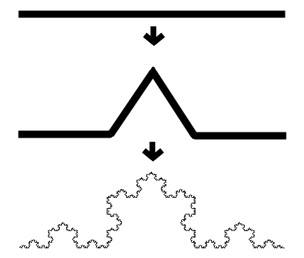
Dengan memperhatikan kurva Koch, kita bisa lihat bahwa kurva tersebut terbagi menjadi 4 pecahan kecil. Setiap pecahan memliki panjang 1/3 dari panjang asal. Kita bisa tetapkan $latex N=4$ dan $latex S=3$ sehingga memberikan dimensi fraktal sebesar 1,231. Nilai dimensi pecahan ini (yang bukan bilangan bulat) membuat kurva Koch digolongkan sebagai sebuah fraktal.
Bagaimana dengan Mandelbrot Set dan Sierpinski Pyramid yang diberikan di awal tulisan? Dapatkah teman-teman menghitung berapa dimensinya? Coba sendiri, ya. ;)
Oya, ada satu hal yang hampir terlupakan untuk disampaikan. Banyak sekali contoh fraktal yang ada di alam sekitar kita. Bentuk garis pantai, jalur aliran sungai, daun-daun pohon cemara, hingga pola motif batik pun bisa dijelaskan dengan konsep fraktal. Dengan demikian, eksplorasi fraktal sebenarnya tak terbatas pada definisi matematis belaka. Imajinasi kitalah yang menjadi batasnya.
Bahan bacaan:
- Rujukan utama artikel ini: http://davis.wpi.edu/~matt/courses/fractals/intro.html
- Gambar Mandelbrot Set dan Sierpinski Pyramid: http://en.wikipedia.org/wiki/Fractal
- http://fraktal.bandungfe.net/
- Tulisan tentang fraktal pada laman Wolfram MathWorld: http://mathworld.wolfram.com/Fractal.html
Penulis:
Isnie Yusnitha, staf Universitas Pendidikan Indonesia, Bandung.
Kontak: isnie.yusnitha(at)gmail(dot)com



