Penggunaan konsep matematika untuk memahami laju penularan penyakit sudah cukup lama dilakukan. Adalah Bernoulli (ya, Bernoulli yang juga menemukan persamaan Bernoulli di fisika) yang diketahui pertama kali menggunakan persamaan matematika untuk mempromosikan inokulasi massal sebagai upaya kesehatan masyarakat untuk mengurangi kematian akibat penyakit cacar (smallpox) di Eropa abad ke-18 saat vaksinasi belum dikenal di masa tersebut.
Di dalam tulisan ini akan dibahas satu konsep matematika yang sangat mendasar di dalam memahami laju penyebaran penyakit menular, yaitu konsep ‘angka reproduksi dasar‘ atau di dalam bahasa Inggris dikenal sebagai ‘basic reproductive number‘, simbolnya $latex R_0$ (dibaca: ar-zero atau ar-naught). $latex R_0$ adalah rata-rata jumlah orang yang akan terinfeksi oleh satu kasus infeksi baru di dalam populasi yang tidak memiliki kekebalan terhadap infeksi tersebut. Misalnya, penyakit cacar memiliki $latex R_0 =3$, artinya satu kasus cacar rata-rata akan menulari tiga orang, sedangkan polio mempunyai $latex R_0$ sebesar 4 s.d. 6, artinya satu kasus polio akan menular dan menghasilkan rata-rata empat sampai enam kasus baru. Dengan menggunakan bilangan ini kita dapat mengatakan banyak hal tentang penyebaran penyakit.
Berapa banyak orang yang akan jatuh sakit pada suatu kejadian luar biasa/epidemi?
Untuk penyakit-penyakit yang ditularkan secara langsung dari orang-ke-orang, perkiraan besarnya epidemi bisa diperkirakan dengan menyelesaikan persamaan berikut
$latex \ln(s) = R_0 (s – 1)$,
dengan $latex s$ adalah proporsi penduduk yang ‘selamat’ dari suatu epidemi, yakni proporsi penduduk yang tidak terserang penyakit di saat epidemi berakhir.
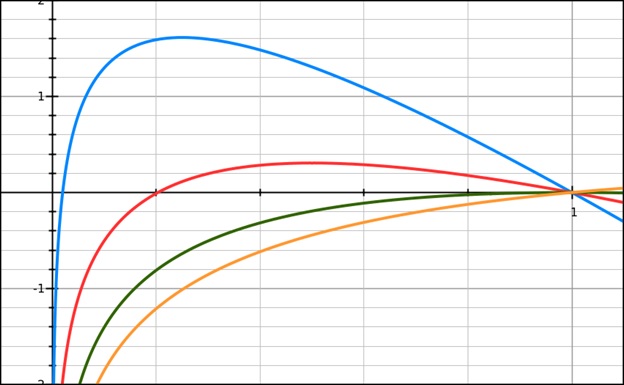
Berdasarkan plot $latex \ln(s) = R_0 (s – 1)$, besaran $latex x$ yang memiliki nilai $latex y = 0,$ dan dengan syarat $latex 0 < x < 1,$ adalah proporsi orang yang tidak terserang penyakit di akhir epidemi. Untuk $latex R_0 = 4$, grafik memotong sumbu-x pada $latex x = 0,02$. Artinya, jika satu penyakit menular dengan $latex R_0 = 4$ ditularkan ke suatu populasi yang tidak memiliki kekebalan, akan terjadi wabah yang akan menyerang 98% anggota populasi tersebut (2% akan lolos dari penyakit). Semakin kecil $latex R_0$, bagian kurva di sebelah kiri $latex x = 1$ akan bergeser ke kanan sehingga akhirnya pada saat $latex R_0 = 1$ kurva hanya akan memotong sumbu-x pada titik $latex x = 1$. Dengan demikian, penyakit menular dengan $latex R_0 = 1$ tidak dapat menyebabkan wabah.
Penjelasannya sebagai berikut, karena $latex R_0$ menggambarkan jumlah infeksi baru yang bisa disebabkan oleh satu kasus infeksi yang ada, dengan $latex R_0 = 4$ satu kasus akan menulari 4 orang. Lalu, setiap kasus baru ini akan menulari 4 orang berikutnya, berikutnya, dan seterusnya sampai akhirnya tidak ada orang yang bisa tertulari. Dengan kata lain, jumlah orang yang terinfeksi akan mengikuti deret: 1, 4, 16, 64, 256, dst.
Dari penjelasan tersebut, jika $latex R_0 = 1$ deret tersebut akan menjadi: 1, 1, 1, 1, dst. Dengan kata lain, penyakit menular dengan $latex R_0 = 1$ tidak akan menyebabkan ledakan kasus, tapi akan bertahan di suatu populasi sebagai penyakit yang endemis. Jika $latex R_0$ turun sampai di bawah 1, penyakit tersebut akan hilang dari populasi tersebut atau punah. Dengan demikian, pengetahuan tentang $latex R_0$ dapat digunakan dengan tujuan pengendalian penyakit menular, yaitu untuk menurunkan $latex R_0$ menjadi lebih kecil dari 1.
Memahami komponen-komponen membantu kita menentukan metode pengendalian penyakit yang paling baik
Penyakit ditularkan melalui suatu proses. Sebagai ilustrasi, katakan seorang bernama A menderita suatu penyakit menular yang disebabkan oleh virus V. Pertama-tama, virus akan memasuki tubuh A, misalnya melalui saluran pernapasan, lalu virus akan berkembang biak sebelum akhirnya A jatuh sakit dan atau bisa menularkan virus V ke orang lain. Periode waktu sejak virus masuk sampai A jatuh sakit disebut sebagai masa inkubasi, sedangkan periode waktu sejak virus masuk ke dalam tubuh sampai bisa ditularkan lagi disebut masa laten. Panjangnya masa laten bisa berbeda dengan masa inkubasi, bisa lebih singkat, bisa lebih panjang. Setelah masa laten dilalui, A akan memasuki masa infeksius dan dapat menularkan virus V sampai akhirnya A sembuh (atau meninggal dunia).
Bayangkan apa yang terjadi di masa infeksius. A mungkin cukup sehat untuk berjalan-jalan di mal, pasar, bermain catur, atau sekedar bercakap-cakap dengan teman-teman dan anggota keluarganya. Dengan kata lain, di dalam masa infeksius tersebut A dapat melakukan kontak dengan sejumlah orang. Di dalam setiap kesempatan kontak ini, ada kemungkinan A menularkan virus V kepada orang di sekitarnya. Tentunya besaran kemungkinan, probabilitas, penularan ini tidak sama antara satu jenis kontak ke jenis kontak yang lain. Misalnya, kemungkinan penularan dari kontak A dengan seorang kasir di mal akan berbeda dengan kemungkinan penularan dari kontak A dengan orang tuanya di rumah. Sebaliknya, tidak semua kontak berakhir pada penularan. Misalnya, ada kemungkinan A melakukan kontak dengan orang yang ternyata sudah kebal terhadap infeksi virus V karena, misalnya, orang tersebut sudah pernah terinfeksi virus V atau sudah pernah divaksinasi sebelumnya.
Ada 4 komponen yang menentukan besarnya $latex R_0$, yaitu i) lamanya masa infeksius, ii) jumlah kontak, iii) kemungkinan terjadinya penularan pada setiap kontak dan iv) adanya populasi rentan terhadap infeksi. Berdasarkan hal ini, $latex R_0$ bisa diperkecil dengan:
i) Mengurangi masa infeksius: misalnya dengan memberi pengobatan antivirus (atau antibiotik untuk penyakit akibat bakteri). Karantina atau isolasi kasus infeksius juga pada akan mengurangi masa infeksius yang efektif.
ii) Mengurangi jumlah kontak: misalnya dengan menutup sekolah dan tempat umum lain atau dengan mengisolasi kasus infektif. Pada kasus flu burung di Bali bulan April 2012 lalu misalnya, dilakukan penutupan pasar. Strategi ini biasa disebut sebagai social distancing.
iii) Memperkecil kemungkinan terjadinya penularan: misalnya dengan menganjurkan orang mengenakan masker untuk mencegah penularan flu. Vaksinasi, walaupun tidak memberikan perlindungan 100% juga tetap bermanfaat untuk mengurangi penularan penyakit.
iv) Memperkecil jumlah orang yang rentan terhadap penyakit: misalnya dengan vaksinasi massal. Semakin banyak orang yang kebal terhadap penyakit, semakin kecil kemungkinan penyakit bisa menyebar karena orang-orang yang sudah kebal seolah-olah menjadi tembok yang menghalangi penularan. Vaksinasi memang menjadi primadona pengendalian penyakit menular karena dengan meningkatkan kekebalan populasi (istilahnya: herd immunity), suatu penyakit bisa ditekan sampai kurang dari satu dan akhirnya penyakit tersebut bisa dihilangkan dari muka bumi. Penyakit cacar adalah penyakit yang telah berhasil dihilangkan sifat wabahnya dari muka bumi dengan vaksinasi.
$latex R_0$ menentukan proporsi penduduk yang harus divaksinasi/cakupan minimal vaksinasi.
Kembali ke definisi dari $latex R_0$, besaran $latex R_0$ adalah jumlah rata-rata infeksi baru akibat satu kasus infeksius pada populasi yang sepenuhnya rentan. Jika sebagian orang di dalam suatu populasi sudah memiliki kekebalan, tidak rentan, besaran $latex R_0$ akan berkurang. Besaran tersebut sekarang kita sebut sebagai angka reproduksi efektif $latex (R_e)$ sehingga
$latex R_e = R_0 \times s$,
dengan $latex s$ adalah proporsi penduduk yang rentan terhadap penyakit. Sebagai contoh, jika semua orang di dalam satu populasi masih rentan terhadap penyakit V, maka $latex s$ di sini adalah 1 sehingga $latex R_e = R_0 \times 1$ atau sama dengan $latex R_0$ itu sendiri. Jika seperempat populasi sudah kebal terhadap penyakit V, kita peroleh $latex R_e = R_0 \times (3/4)$.
Kembali ke prinsip pengendalian penyakit menular, karena kita ingin agar $latex R_0$ lebih kecil dari satu, proporsi minimal yang harus diimunisasi bisa diperkirakan dari besarnya $latex s$ untuk $latex R_e = 1$, yaitu: $latex R_0 \times s$ sehingga $latex s = 1/R_0$. Karena $latex s = 1/R_0$ adalah proporsi penduduk yang masih rentan pada saat $latex R_e = 1$, maka proporsi penduduk yang harus dibuat kebal/diimunisasi agar $latex R_e = 1$ adalah setidaknya sebesar $latex 1 – 1/R_0$.
Sebagai contoh, untuk suatu penyakit dengan $latex R_0 = 4$, proporsi penduduk yang harus diimunisasi adalah $latex 1 – 1/4,$ atau 75%. Untuk penyakit dengan $latex R_0 = 3$, seperti cacar yang sudah berhasil dibasmi, proporsi penduduk yang harus diimunisasi adalah $latex 1 – 1/3 = 67\%$. Namun demikian, perhitungan tersebut hanya berlaku jika vaksinasi yang diberikan memberikan perlindungan 100% terhadap penyakit. Sayangnya kebanyakan vaksin tidak memberikan perlindungan 100%, mungkin hanya sekitar 80% atau 90% sehingga pada umumnya program vaksinasi menargetkan angka cakupan yang tinggi di atas 90%.
Mudah-mudahan tulisan ini dapat membantu menerangkan dinamika penularan penyakit infeksi, khususnya pentingnya angka reproduksi dasar, $latex R_0$. Perlu digarisbawahi bahwa yang diterangkan dalam tulisan ini hanya berlaku jika penyakit ditularkan dari orang ke orang di dalam populasi yang homogen, yaitu populasi yang memiliki karakteristik setiap orang melakukan kontak dengan orang lain dalam kuantitas yang sama. Untuk jenis penyakit lain, seperti demam berdarah yang ditularkan oleh nyamuk, dan pola kontak yang berbeda, seperti penyakit pada anak sekolah yang lebih banyak melakukan kontak dengan usia sebayanya, banyak penyesuaian yang perlu dilakukan terhadap konsep dinamika penularan penyakit tersebut.
Bahan bacaan:
- R. Anderson dan R. May, Infectious Diseases of Humans, Dynamic and Control, Oxford University Press (1992).
Penulis:
Panji Fortuna Hadisoemarto, staf Departemen Ilmu Kesehatan Masyarakat FK Unpad.
Kontak: hadisoemartopanji(at)gmail.com