Kita mengenal sebuah fungsi, misalkan f(x) = ax2 + bx + c. Dengan nilai a, b, dan c tertentu, nilai f(x) dapat dicari untuk setiap nilai x. Akan tetapi, terkadang hidup tidak selalu mudah. Sering kita menemui data-data yang tidak memiliki fungsi eksplisit seperti di atas dan hanya berupa angka-angka di x dan f(x). Biasanya data tersebut dijabarkan dalam suatu bentuk tabel atau grafik. Seringkali dalam tabel tersebut, nilai x terdiri atas deretan bilangan dengan interval tertentu dengan pasangannya f(x) di kolom yang lain. Terkadang kita ingin mengetahui berapakah nilai f(x) pada x yang tidak tidak tercantum pada tabel tersebut. Bagaimana caranya?
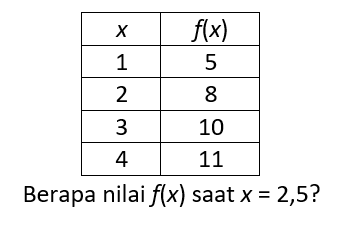
Untuk mengetahui berapa harga fungsi yang tidak dicantumkan di antara dua buah harga yang terdapat pada suatu tabel, ada sebuah metode matematika yang disebut dengan interpolasi. Pada kesempatan ini, kita akan belajar tentang interpolasi linear.
Suatu interpolasi dikatakan merupakan interpolasi linear apabila plot datanya dalam sistem koordinat cartesius mendekati fungsi linear yang grafiknya berbentuk garis lurus.
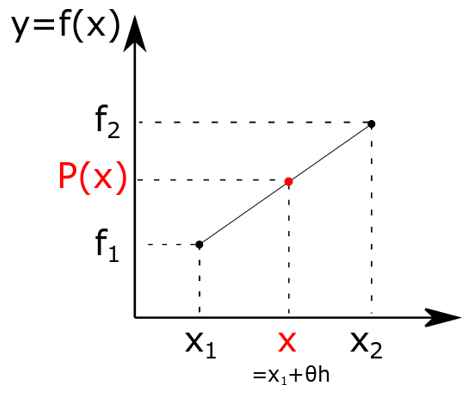
Kurva y = f(x) didekati dengan garis lurus antara x1 dan x2 . Harga fungsi pada x = x1 adalah f(x1) = f1. Harga fungsi pada x = x2 adalah f(x2) = f2.
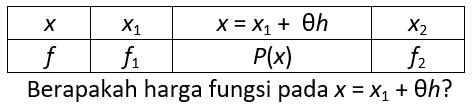
Nilai P(x) didapatkan dengan mengingat persamaan garis linear. Karena garis f(x) pada rentang x1 dan x2 merupakan garis lurus yang kontinu, ia memiliki satu gradien yang sama sehingga
\displaystyle \frac{(P(x)-f_1)}{(x - x_1)} = \frac{f_2 - f_1}{x_2 - x_1} .
Dari sini didapatkanlah persamaan interpolasi linear:
\displaystyle P(x) = f_1 + \displaystyle \frac{x - x_1}{x_2 - x_1} (f_2 - f_1).
Contoh: Hitung y pada x = 2,3 dari tabel data di bawah ini.

Jawab: Plot dulu data tersebut dalam sistem koordinat cartesius untuk memastikan jenis interpolasinya.
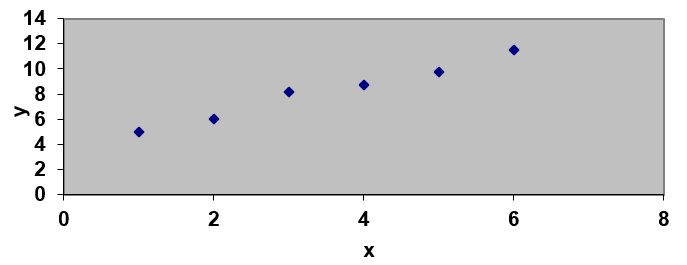
Setelah itu, gunakan rumus interpolasi dan lakukan perhitungan seperti pada skema berikut, dengan nilai yang ingin dicari untuk x = 2,3 berada di antara 2,0 dan 3,0.
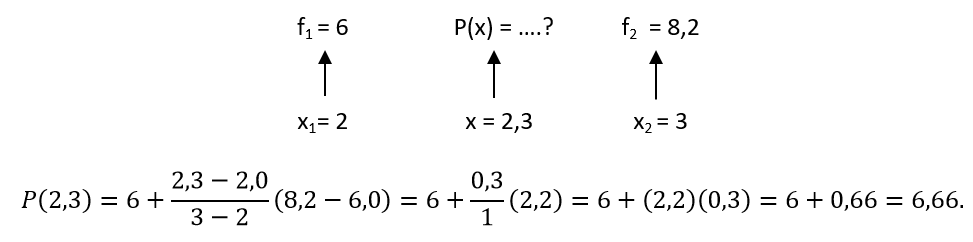
Bagaimana jika gambar kurva titik di atas tidak menunjukkan “kecenderungan” garis lurus? Ada teknik lain seperti interpolasi kuadratik. Kita akan belajar seputar interpolasi kuadratik pada rubrik matematika Majalah 1000guru di edisi terpisah.
Bahan Bacaan:
- Burden , R. L., Numerical Analysis, Boston, 1981.
- Hamming, R.W., Introduction to Applied Numerical Analysis, McGraw Hill, New York, 1987.
Penulis:
M. Nawi Harahap, Widyaiswara Matematika, PPPPTK BBL Medan.
Kontak: mnawiharahap(at)yahoo.com



