Dari sebuah legenda, disebutkan bahwa pada masa perang sekitar abad ke-1, tentara Yahudi pernah terkepung oleh tentara Roma. Mereka kemudian memutuskan sebuah rencana agar tidak tertangkap. Sayangnya, daripada tertangkap, mereka malah merencanakan untuk saling membunuh sesamanya. Caranya, mereka berdiri di dalam suatu lingkaran, orang pertama menusuk teman di sampingnya, berlanjut seterusnya hingga tertinggal satu orang saja yang hidup.
Tidak semua orang setuju dengan rencana gila itu. Ada seorang yang bernama Josephus, tentara Yahudi yang terkepung oleh tentara Roma. Josephus tidak mau mati dan lebih memilih untuk ditangkap oleh tentara Roma. Oleh karenanya, ia harus mencari cara, supaya ia ada di posisi orang yang hidup terakhir. Permasalahan ini, yang populer disebut “The Josephus Problem”, merupakan salah satu contoh soal optimasi di dalam matematika maupun ilmu komputer.
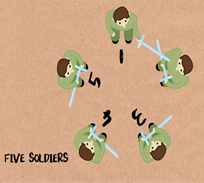
Kita misalkan untuk kasus 5 tentara. Tentara nomor 1 mengeluarkan tentara nomor 2. Kemudian, tentara nomor 3 mengeluarkan nomor 4. Tentara nomor 5 mengeluarkan nomor 1. Tentara nomor 3 mengeluarkan nomor 5. Pada kasus ini, orang yang hidup terakhir adalah orang pada posisi nomor 3.
Sekarang misalkan ada 12 tentara. Tentara nomor berapa yang akan menjadi tentara yang hidup terakhir? Kita bisa buat bagan berikut ini (tanda panah berarti “mengeluarkan”):
1→2, 3→4, 5→6, 7→8, 9→10, 11→12, 1→3, 5→7, 9→11, 1→5, 9→1.
Ya, tentara yang hidup adalah tentara di posisi nomor 9.

Lalu, bagaimana jika dalam satu lingkaran ada lebih dari 50 tentara? 100 tentara? Bagaimana cara Josephus agar ia dapat selalu menjadi tentara terakhir yang hidup? Untuk menyelesaikan masalah ini kita harus melihat pola yang ada. Kita misalkan jumlah tentara dalam satu lingkaran = n, dan tentara yang hidup terakhir misalkan W(n). Untuk beberapa nilai n, kita bisa buat tabel W(n).

Dari pola pada tabel, kita dapat menemukan:
n = 2a + L, dengan L < 2a
sehingga W(n) = 2L + 1.
Pada rumus di atas, a adalah angka yang terbesar yang menghasilkan nilai pangkat 2 mendekati n, dan L adalah sisa dari n – 2a. Supaya lebih jelas, ambil contoh jumlah tentara n = 41. Kita bisa tulis 41 = 25 + 9 sehingga W(n) = (2 × 9) + 1 = 19. Hasilnya, tentara yang hidup terakhir adalah tentara pada posisi 19. Coba teman-teman lakukan untuk angka yang lebih besar seperti 77 dan 89.
Kita juga bisa menggunakan metode notasi bilangan biner untuk masalah ini. Misalkan masih dengan contoh 41 tentara tadi, 41 = 25 + 23 + 20. Di dalam notasi biner, 25 24 23 22 21 20 menjadi 101001. Kita pindahkan angka 1 pertama ke posisi terakhir menjadi 010011 sehingga 24 + 21 + 20 = 16 + 2 + 1 = 19. Wow!
Bahan bacaan:
Penulis:
Evelyn Pratami Sinaga, Alumnus Jurusan Fisika, Tohoku University, Jepang.
Kontak: evelynpratami(at)gmail(dot)com.



