Bilangan segitiga, yang dilambangkan dengan $latex T_n$, merupakan bilangan yang dihasilkan dari menjumlahkan titik-titik yang membentuk segitiga.
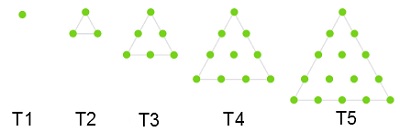
Baris pertama segitiga memiliki satu elemen dan baris selanjutnya memuat satu elemen lebih banyak dari baris sebelumnya, seperti yang diilustrasikan pada gambar di atas. Bilangan segitiga untuk $latex n= 1,2,3,4,\ldots$ adalah
$latex 1,1+2,1+2+3,1+2+3+4,\ldots$
atau
$latex 1,3,6,10,\ldots$
Secara formal, bilangan segitiga adalah bilangan yang didapatkan dari menjumlahkan semua bilangan bulat positif yang kurang dari atau sama dengan bilangan bulat positif $latex n$. Pernyataan ini dapat dituliskan dalam notasi deret:
$latex T_n = \sum_{k=1}^{n} k=\frac{n(n+1)}{2}$
Pernyataan (1) dapat dibuktikan dengan menulis $latex T_n$ sebagai berikut:
$latex T_n= 1+2+3+\ldots +n,$
atau
$latex T_n = n+(n-1) + (n-2) + \dots + 1.$
Kemudian, kedua persamaan di atas dijumlahkan sehingga menjadi
$latex 2T_n = (n+1) +(n+1) + \dots + (n+1).$
Pada ruas kanan persamaan yang terakhir ini, terdapat $latex (n+1)$ sebanyak $latex n$ kali. Dengan demikian,
$latex 2T_n = n(n+1),$
$latex T_n = \frac{n(n+1)}{2}.$
Soal Cerita
Buum! Secara tiba-tiba, sebuah pesawat harus melakukan pendaratan darurat di sebuah gurun pasir. Untunglah Dani, sang pilot, selamat dalam kecelakaan tersebut. Dani mengetahui ada sebuah desa yang dapat dijangkau di sekitar daerah itu, tetapi dia tidak tahu arah mana yang harus diambil. Untuk itu, dengan lihai dia menjalankan sebuah rencana berbekal sebuah kompas.
Dani berjalan 1 km ke arah utara, kemudian berganti arah ke timur sejauh 2 km, kemudian 3 km ke arah selatan, 4 km ke arah barat, 5 km ke arah utara, 6 km ke arah timur, dan seterusnya, seperti pada gambar.
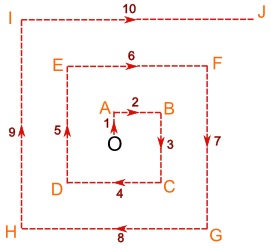
Dengan cara ini, Dani akan menemukan desa tersebut walaupun Dani tidak mengetahui letaknya. Tetapi untuk menemukan jalan kembali ke pesawat, jika sewaktu-waktu dibutuhkan, Dani perlu menghitung seberapa jauh ia telah berjalan.
Ketika Dani telah mencapai titik A, Dani telah berjalan sejauh 1 km. Ketika berada pada titik B, Dani telah menempuh 3 km. Dan ketika di titik C, Dani telah menempuh jarak 6 km. Nah, mari kita hitung bersama untuk titik-titik yang selanjutnya dengan mengisi tabel berikut ini!
| Titik | Jarak yang Telah Ditempuh |
| O | 0 |
| A | 1 |
| B | 3 |
| C | 6 |
| D | … |
| E | … |
| F | … |
| G | … |
| H | … |
| I | … |
| J | … |
Setelah selesai menghitung, dapat diamati pada setiap tahap, total jarak merupakan penjumlahan dari $latex 1+2+ \ldots + n,$ yang berarti permasalahan yang dihadapi Dani dapat dikerjakan dengan menggunakan bilangan segitiga atau persamaan (1). Mari kita hitung lagi!
| Titik | $latex n$ | Jarak yang Telah Ditempuh |
| O | 0 | $latex T_n = \frac{n(n+1)}{2} = \frac{0 \times 1}{2} = 0$ |
| A | 1 | $latex T_n = \frac{n(n+1)}{2} = \frac{1 \times 2}{2} = 1$ |
| B | 2 | $latex T_n = \frac{n(n+1)}{2} = \frac{2 \times 3}{2} = 3$ |
| C | 3 | $latex T_n = \frac{n(n+1)}{2} = \frac{3 \times 4}{2} = 6$ |
| D | 4 | … |
| E | 5 | … |
| F | 6 | … |
| G | 7 | … |
| H | 8 | … |
| I | 9 | … |
| J | 10 | … |
Setelah selesai menghitung, bandingkan hasilmu untuk kedua tabel yang telah dikerjakan. Apakah hasilnya sama?
Relasi
Ternyata bilangan segitiga memiliki relasi dengan bilangan-bilangan yang lain sepertibilangan pentagonal ($latex P_n$) dan heksagonal ($latex H_n $). Selain itu, penjumlahan dari dua bilangan segitiga berturut-turut merupakan bilangan kuadratik. Bagaimana bisa? Mari kita lihat!
Bilangan pentagonal memiliki definisi sebagai berikut:
$latex P_n = \frac{n(3n-1)}{2}.$
Kita coba cari hubungan antara bilangan segitiga dan pentagonal melalui perhitungan berikut ini:
$latex P_n = \frac{n(3n-1)}{2} = \frac{3}{3} \times \frac{n(3n-1)}{2} = \frac{1}{3} \times \frac{(3n-1)3n}{2} = \frac{1}{3} T_{3n-1}$
Jadi, relasi antara bilangan segitiga dan pentagonal adalah
$latex P_n = \frac{1}{3} T_{3n-1}$
Sekarang, kita cek hubungan antara bilangan segitiga dan heksagonal. Bilangan heksagonal memiliki definisi sebagai berikut:
$latex H_n = n(2n-1)$
Lakukan perhitungan yang serupa seperti sebelumnya:
$latex H_n = n(2n-1) = \frac{1}{2}(2n-1)((2n-1)+1) = \frac{(2n-1)2n}{2} = T_{2n-1}$
Jelas terlihat bahwa hubungan antara bilangan segitiga dan heksagonal adalah:
$latex H_n = T_{2n-1}$
Selanjutnya, bagaimana caranya membuktikan bahwa penjumlahan dari dua bilangan segitiga berturut-turut merupakan bilangan kuadratik? Teman-teman bisa coba hitung juga:
$latex T_{n-1}+T_n = \frac{(n-1)n}{2} + \frac{n(n+1)}{2}$
$latex =\frac{1}{2} n((n-1) + (n+1)),$
$latex =\frac{1}{2} n(2n),$
$latex =n^{2}.$
Asyik, kan? Nah, relasi-relasi yang dibahas di sini hanyalah secuplik dari sekian banyak relasi lainnya. Misalnya, kita bisa temukan pula contoh yang lain adalah hubungan bilangan segitiga dengan bilangan kubik atau bilangan tetrahedral. Jangan lupa untuk dieksplorasi sendiri, ya! Semangat belajar!
Bahan bacaan:
- http://mathworld.wolfram.com/TriangularNumber.html
- http://www.mathsisfun.com/algebra/triangular-numbers.html
- http://www.mathematische-basteleien.de/triangularnumber.htm
- http://www.mathsisfun.com/activity/walk-in-desert.html
- http://mathworld.wolfram.com/PentagonalNumber.html
- http://mathworld.wolfram.com/HexagonalNumber.html
Penulis:
Reyna Marsya Quita, mahasiswi master di Jurusan Matematika, Universitas Brawijaya.
Kontak: reynaquita2905(at)gmail(dot)com.



