Ebola dan Matematika

Kurang lebih enam bulan pada tahun 2014, dunia dihebohkan dengan wabah mematikan, Ebola, yang tersebar di Afrika Barat. Virus itu dibawa oleh kelelawar pemakan buah dengan probabilitas kematian 25% hingga 90% bagi manusia yang pernah terjangkit virus tersebut [data WHO, 2014]. Virus ebola dapat menular melalui cairan tubuh maupun kontak langsung dengan pengidap. Tercatat korban yang terjangkit ebola berkembang dari 1000 kasus pada Juli 2014 menjadi 9000 kasus pada Oktober 2014 [dari majalah Science, 2014].

Dalam hal inilah matematika perlu bermain untuk memberikan gambaran bagaimana prediksi penyebaran virus ini. Model S-I-R (susceptible-infectious-recovered) adalah suatu model matematika yang biasa digunakan untuk menggambarkan dinamika penyebaran penyakit. Ada tiga variabel utama dalam model ini, yaitu

S (susceptible) menggambarkan berapa banyak orang sehat yang berpotensi terjangkit penyakit.
I (infectious) menggambarkan jumlah orang yang sedang terjangkit dan berpotensi untuk menyebarkan virus.
R (recovered) menggambarkan jumlah orang “sembuh” atau tidak menularkan virus lagi. Dalam hal ini kita anggap orang tersebut mati atau pulih total.

Ketiga variabel tersebut saling terkait sebagai fungsi waktu. Laju perubahan S dapat dituliskan ke dalam persamaan diferensial berikut ini:

$latex \displaystyle \frac{dS(t)}{dt}=-\frac{\beta I(t) S(t)}{N} \quad \ldots (1)$

Parameter β dalam persamaan di atas menggambarkan jumlah rata-rata berapa orang saling kontak satu sama lain di dalam suatu populasi per hari. Misalkan penduduk Jakarta, yang memiliki kepadatan penduduk 19 ribu jiwa/km² memiliki koefisien β yang lebih besar dibandingkan penduduk Jayapura yang kepadatan penduduknya hanya 200 jiwa/km².

Persamaan menunjukkan bahwa jumlah penduduk yang sehat (S) akan berkurang (perhatikan tanda minus di ruas kanan) seiring meningkatnya jumlah penduduk yang terinfeksi. Di ruas kanan terdapat faktor S(t)/N yang menggambarkan jika jumlah penduduk yang sehat makin sedikit, laju penurunan jumlah orang yang sehat juga mengecil karena orang yang sudah terinfeksi dianggap tidak dapat terinfeksi lagi. Seiring berjalannya waktu, dS(t)/dt dipastikan bernilai nol yang berarti bahwa penyebaran virus sudah berhenti.

Kemudian, untuk jumlah penduduk yang “sembuh” (R), variabel ini akan meningkat bila makin banyak orang yang terinfeksi. Dalam bentuk persamaan, pernyataan tersebut dapat dituliskan sebagai

$latex \displaystyle \frac{dR(t)}{dt} = \gamma I(t) \quad\ldots(2)$

Parameter γ di sini menggambarkan jumlah orang “sembuh” dari virus per hari. Makin cepat virus itu membuat orang “sembuh” makin besar nilai koefisien γ. Kasus terburuk adalah ketika jumlah kontak β sangat besar dan kecepatan “sembuh” γ kecil, yang artinya virus makin menyebar dengan cepat.

Jumlah penduduk total N = S(t) + I(t) + R(t) dianggap tidak berubah dengan mengabaikan perubahan penduduk karena migrasi. Dengan kata lain, dN/dt = 0, sehingga kita dapat tuliskan

$latex 0 = \displaystyle \frac{dS(t)}{dt} + \frac{dI(t)}{dt} + \frac{dR(t)}{dt}$

Atau, setelah substitusikan persamaan (1) dan (2), kita peroleh

$latex \displaystyle \frac{dI(t)}{dt} = \frac{\beta I(t) S(t)}{N} – \gamma I(t) \quad \ldots (3)$

Sekarang mari kita lakukan studi kasus. Misalkan di suatu negara A yang memiliki populasi 7,9 juta jiwa ditemukan 10 orang yang terjangkit ebola. Pada waktu itu, belum terdapat korban meninggal. Jika virus itu dapat disembuhkan selama 3 hari pertolongan dan kemungkinan setiap orang yang terinfeksi akan menyebarkan ke satu orang lain dalam waktu 2 hari, berapakah jumlah orang yang tidak terjangkit virus di daerah tersebut selama 100 hari?

Dari soal di atas, kita mengetahui bahwa pada saat t = 0 hari dapat dituliskan:

S(0) = N = 7.900.000 jiwa
I(0) = 10 jiwa
β = 1/2 hari^-1γ = 1/3 hari^-1

Dengan menyelesaikan persamaan (1)-(3) secara simultan menggunakan metode Runge-Kutta, kita akan mendapatkan plot grafik S(t), I(t), dan R(t).

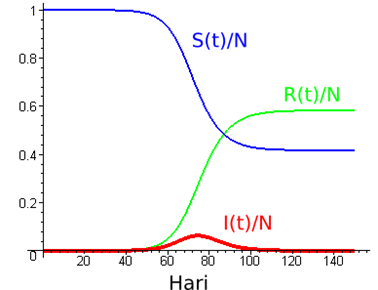
Grafik S(t), I(t), dan R(t). Sumber: math.duke.edu

Dari plot ini dapat kita ketahui bahwa setelah 100 hari hanya sekitar 40% jumlah penduduk yang tidak terjangkit virus ebola. Pada hari ke-100, jumlah orang yang “sembuh” bernilai 60%. Ada kemungkinan dari 60% tersebut 90%-nya meninggal karena pertolongan medis tidak sanggup menyelamatkan nyawa korban.

Nah, dari tulisan sederhana ini kita belajar bagaimana matematika dapat membantu untuk memodelkan dinamika penyebaran penyakit. Dari model ini kita belajar bahwa cara yang tepat untuk menghindar dari penyakit menular adalah mengurangi kontak dengan sumber penyakit dan segera mendapatkan pertolongan bila gejala penyakit mulai terlihat.

Bahan bacaan:

Penulis:
Eddwi Hesky Hasdeo, Peneliti di Lembaga Ilmu Pengetahuan Indonesia.
Kontak: heskyzone(at)gmail(dot)com.

Ebola dan Matematika