Pernahkah teman-teman mempelajari sifat suatu fungsi yang periodik? Contoh fungsi periodik di antaranya adalah fungsi sinus dan cosinus. Nah, dalam kesempatan kali ini kita akan mempelajari penggabungan fungsi-fungsi periodik sinus dan cosinus. Menariknya, suatu fungsi tertentu dapat dinyatakan sebagai deret fungsi trigonometri yang sifatnya periodik. Deret tersebut dinamakan deret Fourier. Fungsi yang dapat dinyatakan dalam deret Fourier adalah fungsi periodik.
Fungsi Periodik
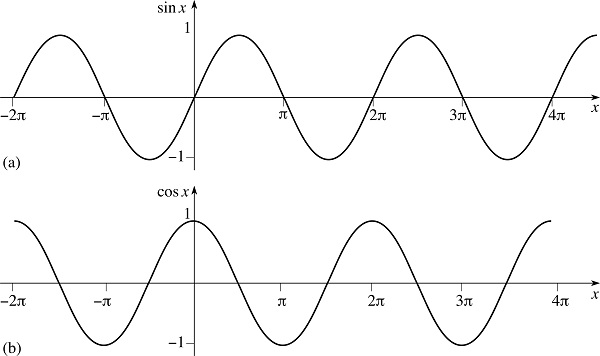
Banyak permasalahan dalam matematika, fisika, dan rekayasa (teknik) melibatkan fungsi periodik, seperti kelistrikan, bunyi, getaran, dan hantaran panas. Fungsi periodik adalah fungsi yang berulang dengan pola tertentu. Dalam bahasa matematis, suatu fungsi dikatakan periodik jika fungsi tersebut memenuhi hubungan $latex f(x) = f(x + L)$, dengan L adalah periode fungsi. Salah satu contoh fungsi periodik yang paling mudah adalah fungsi trigonometri seperti fungsi sinus. Fungsi trigonometri memiliki periode sebesar $latex 2\pi$, sehingga $latex \sin(x) = \sin(x + 2\pi)$. Oleh karena itu, dalam analisis fungsi periodik kita hanya perlu menganalisis fungsi dalam satu periode saja.
Deret Fourier
Suatu fungsi periodik dapat dinyatakan sebagai deret tak hingga dari fungsi trigonometri sinus dengan amplitudo dan fase yang berbeda-beda. Suatu fungsi periodik $latex f(x)$ dapat dituliskan sebagai
$latex f(x) = \sum_{\rm n=0}^{\infty}A_{n}\sin(nx+\Phi_n)$
Karena
$latex \sin(nx+\Phi_n) = \sin(nx)\cos(\Phi_n) + \cos(nx)\sin(\Phi_n)$ ,
kita bisa mengekspresikan fungsi periodik sebagai penjumlahan dari fungsi sinus dan cosinus,
$latex f(x) = \frac{a_0}{2} + \sum_{\rm n=1}^{\infty}(a_{n}\cos(nx) + b_{n}\sin(nx))$
Deret tersebut disebut deret Fourier. Tiap suku dalam deret Fourier memiliki periode $latex \frac{2\pi}{n}$.
Sebagai contoh, mari kita ambil suatu fungsi “gergaji” $latex g(x)$ dengan periode $latex 2\pi$ .
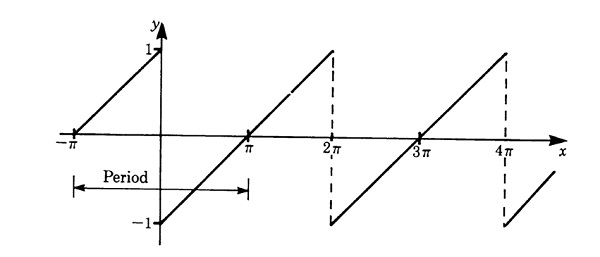
Definisi $latex g(x)$ di sini adalah:
$latex g(x) = \begin{cases} \frac{1}{\pi}x + 1, & -\pi \leq x \leq 0 \\ \frac{1}{\pi}x – 1, &\ \ \ 0\leq x \leq \pi \end{cases}$
Fungsi gergaji tersebut dapat dinyatakan dalam deret Fourier sebagai:
$latex f(x) = -\frac{2}{\pi} \sum_{\rm n=1}^{\infty} \frac{\sin(nx)}{n}$
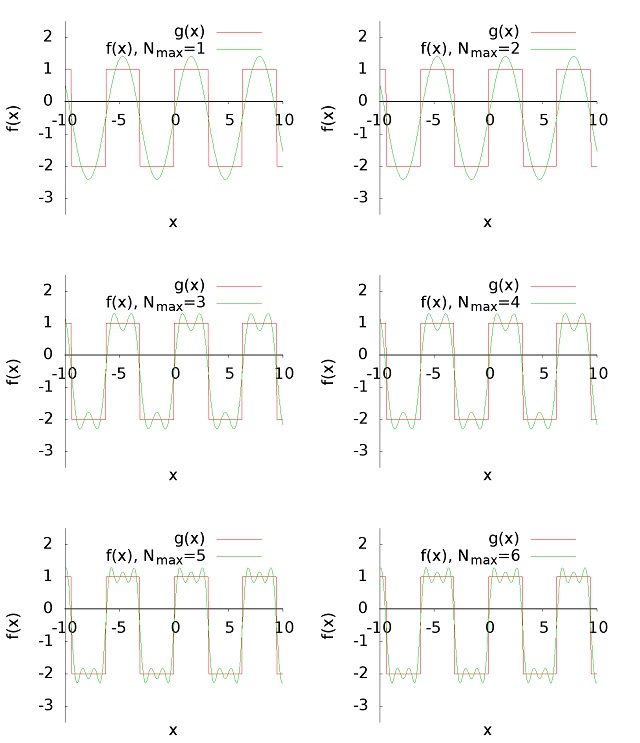
Sekarang kita coba memasukkan nilai $latex n$ dari 1 hingga 6 ke dalam deret Fourier di atas dan kita lihat apa yang akan terjadi.

Semakin besar nilai deret yang kita masukkan ke dalam rumus di atas, bentuk fungsi $latex f(x)$ akan makin menyerupai $latex g(x)$. Namun, fungsi $latex f(x)$ tidak sanggup mengikuti bentuk $latex g(x)$ yang diskontinu pada $latex x = -\pi, x = 0,$ dan $latex x = \pi$. Keterbatasan ini disebut sebagai “fenomena Gibbs”.
Nah! Sekarang kita akan belajar bagaimana menentukan suatu nilai koefisien Fourier sehingga kita dapat menggantikan fungsi $latex g(x)$ dengan deret Fourier $latex f(x)$. Jika suatu fungsi memiliki periode $latex 2\pi$, maka koefisien Fourier $latex a_{0}, a_{n},$ dan $latex b_{n}$ dapat dinyatakan sebagai berikut:
$latex a_{0} = \frac{1}{\pi} \int_{-\pi}^{\pi} g(x)dx$
$latex a_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} g(x)cos(nx)dx$
$latex b_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} g(x)sin(nx)dx$
dengan $latex n = {\rm 1,2,3,}\ $… (bilangan asli).
Pertama, koefisien Fourier ditentukan. Fungsi gergaji merupakan fungsi ganjil karena $latex g(-x) = -g(x)$. Koefisien fungsi genap $latex a_{0},\ a_{n}$ bernilai nol karena integral fungsi ganjil dalam satu periode adalah nol. Dengan demikian, hanya $latex b_{n}$ saja yang dibutuhkan.
$latex b_{n} = \frac{1}{\pi} \int_{-\pi}^{0} (\frac{x}{\pi} + 1)\sin(nx)dx + \frac{1}{\pi} \int_{0}^{\pi} (\frac{x}{\pi} – 1)\sin(nx)dx$
$latex = \frac{1}{\pi^{2}} \int_{-\pi}^{\pi} x\sin(nx)dx + \frac{1}{\pi}\int_{-\pi}^{0}\sin(nx)dx – \frac{1}{\pi}\int_{0}^{\pi}\sin(nx)dx$
$latex = -\left [ \frac{1}{\pi^{2}n}x\cos(nx)\right]_{-\pi}^{\pi} + \left [ \frac{1}{\pi^{2}n}\sin(nx)\right]_{-\pi}^{\pi} – \left [ \frac{1}{\pi n}\cos(nx)\right]_{-\pi}^{0} + \left [ \frac{1}{\pi n}\cos(nx)\right]_{0}^{\pi}$
$latex = -\frac{2}{\pi n}$
Fungsi gergaji tersebut kemudian dapat dinyatakan dalam deret Fourier sebagai:
$latex f(x) = -\frac{2}{\pi} \sum_{\rm n = 1}^{\infty}\frac{\sin(nx)}{n}$
Bentuk fungsi $latex f(x)$ ini persis seperti yang telah ditulis sebelumnya.
Contoh yang lain adalah fungsi kotak. Ayo teman-teman silakan coba juga sendiri di rumah. Pertama-tama kita perlu definisikan fungsi $latex g(x)$ -nya kemudian cari koefisien-koefisien Fourier dari fungsi tersebut.
Bila fungsi periodik memiliki periode selain $latex 2\pi$, semisal $latex 2L$, fungsi tersebut tetap dapat dinyatakan dalam deret Fourier dengan koefisien Fourier sebagai berikut:
$latex a_{0} = \frac{1}{L} \int_{-L}^{L} f(x)dx$
$latex a_{n} = \frac{1}{L} \int_{-L}^{L} f(x)\cos(\frac{n\pi}{L}x)dx$
$latex b_{n} = \frac{1}{L} \int_{-L}^{L} f(x)\sin(\frac{n\pi}{L}x)dx$
Sebagai contoh, terdapat fungsi kotak dengan periode 4:
$latex f(x) = \begin{cases} 0, & -2 < x \leq 0 \\ 1, &\ \ \ 0 < x \leq 2 \end{cases}$
Hitung:
$latex a_{0} = \frac{1}{2} \int_{0}^{2} dx = 1$
$latex a_{n} = \frac{1}{2} \int_{0}^{2} \cos\frac{n\pi x}{2}dx = 0$
$latex b_{n} = \frac{1}{2} \int_{0}^{2} \sin\frac{n\pi x}{2}dx = \frac{1}{n\pi} (1-\cos n\pi)$
Kita peroleh:
$latex f(x) = \frac{1}{2} + \frac{2}{\pi}(\sin\frac{\pi x}{2} + \frac{1}{3}\sin\frac{3\pi x}{2} + \frac{1}{5}\sin\frac{5\pi x}{2} +$ … $latex )$
Transformasi Fourier
Suatu fungsi dengan periode tertentu dapat dinyatakan dalam deret Fourier. Tetapi, bagaimana dengan fungsi yang memiliki periode tak berhingga atau dengan kata lain tidak periodik? Kita dapat menganggap fungsi tersebut sebagai fungsi periodik dengan periode tak terhingga dan mengganti penjumlahan pada deret Fourier dengan integral. Metode ini disebut transformasi Fourier. Sebagai contoh, kita dapat menganalisis sinyal seperti bunyi yang pada awalnya merupakan fungsi waktu, diubah sebagai fungsi frekuensi dengan memanfaatkan transformasi Fourier. Kita kemudian dapat melihat periodisitas sinyal tersebut setelah sinyal tersebut ditransformasi.
Jika kita memiliki suatu fungsi $latex f(x)$, transformasi Fourier dari fungsi tersebut adalah
$latex g(k) = \int_{-\infty}^{\infty} f(x) e^{-ikx} dx$
$latex f(x) = \int_{-\infty}^{\infty} \frac{g(k)}{2\pi} e^{ikx} dx$
Sebagai contoh, terdapat suatu fungsi
$latex f(x) = \begin{cases} 1 & (-a < x < a) \\ 0 &\ \ \ \ \ \ {\rm (lainnya)} \end{cases}$
Transformasi dari fungsi tersebut adalah
$latex g(k) = \int_{-a}^{a} e^{-ikx} 1 dx = \frac{1}{-ik} \left [ e^{-ika} – e^{ika} \right ] = \frac{2\ \sin ka}{k}$
Rangkuman dan Manfaat
Fungsi periodik adalah fungsi yang berulang dengan pola tertentu. Suatu fungsi periodik dapat diuraikan dalam bentuk deret Fourier. Semakin banyak suku dalam deret Fourier, maka semakin bagus deret tersebut mendekati fungsi yang diuraikan. Fungsi dengan periode tak terhingga atau tidak periodik dapat juga diuraikan dengan deret Fourier, tetapi penjumlahan pada deret digantikan dengan integral. Metode ini dinamakan Transformasi Fourier. Manfaat dari deret Fourier adalah seperti dalam analisis gelombang bunyi, vibrasi, optika, maupun pengolahan citra seperti dalam pencitraan medis.
Setelah membaca artikel ini, sangat disarankan bagi teman-teman membuka animasi deret Fourier di falstad.com/fourier/ untuk memahami berbagai macam bentuk fungsi yang dibentuk dari gabungan fungsi sinus dan cosinus dalam deret Fourier.
Bahan bacaan:
- http://mathworld.wolfram.com/FourierSeries.html
- http://mathworld.wolfram.com/FourierTransform.html
- http://www.theFouriertransform.com/
- http://www.falstad.com/fourier/
Penulis:
Muhammad Shoufie Ukhtary, mahasiswa doktor di Departemen Fisika, Tohoku University, Jepang.
Kontak: muhamadukhtary(at)gmail(dot)com.