Mungkin kita sudah tidak asing dengan matematika yang gemar menyelipkan huruf di dalam sebuah persamaan. Alfabet, seperti a, b, c, x, y, masing-masing merepresentasikan sebuah angka, atau dalam kasus tertentu, barisan angka dalam sebuah kisaran. Representasi seperti ini adalah esensi dari apa yang disebut aljabar biasa (anak gaul sekarang bilangnya “b aja”).
Walaupun penggunaan alfabet ini terlihat njlimet dan tidak pada tempatnya (masa belajar angka pake huruf, sih?), ini merupakan sebuah langkah besar bagi para matematikawan, lo! Ada aljabar biasa, berarti ada aljabar luar biasa, dong? Ya, ada!
Dalam aljabar luar biasa, atau aljabar beberapa dimensi, kita berhadapan dengan banyak angka sekaligus yang disusun dalam posisi yang bisa dispesifikasi oleh baris dan kolom. Mari lihat contoh di bawah yang berisi angka-angka dalam satu kesatuan A, atau biasa disebut matriks A.
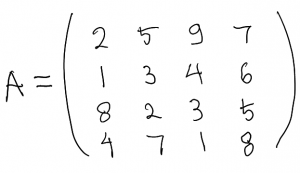
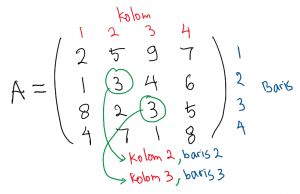
Matriks A di atas terdiri dari 4 kolom dan 4 baris, atau bisa disebut sebagai matriks orde/ukuran 4×4 (baris × kolom). Kolom adalah posisi angka secara horizontal dihitung dari angka pertama di posisi paling kiri atas. Baris adalah posisi angka secara vertikal dari acuan yang sama. Masing-masing angka mempunya posisi yang dipetakan oleh dua “koordinat” tersebut. Contoh: angka 3 ada di kolom kedua – baris kedua dan kolom ketiga – baris ketiga.
Pada prinsipnya, sebuah matriks dapat berisikan angka beribu-ribu dengan beratus-ratus kolom dan baris. Sebuah matriks dapat diperlakukan seperti sebuah angka, tidak peduli berapa isi komponen di dalamnya. Mengoperasikan satu matriks dengan matriks lainnya pun menggunakan beberapa prinsip yang sama dengan aljabar biasa. Mari kita lihat contoh operasi di matriks, untuk menjumlahkan matriks A dan B.
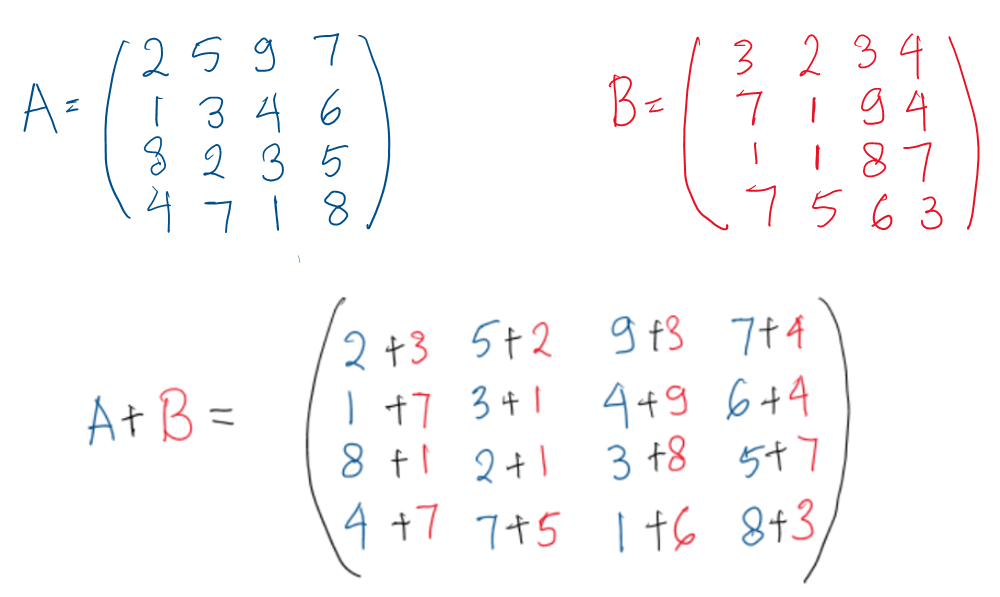
Seperti yang bisa kita lihat di atas, penjumlahan yang terjadi adalah antarmatriks, angka dalam posisi yang sama di keduanya. Atas dasar prinsip inilah, untuk dua atau lebih matriks bisa dijumlahkan, diperlukan jumlah kolom dan baris, atau singkatnya, ukuran, yang sama. Operasi pengurangan juga menggunakan prinsip yang sama dengan penjumlahan.
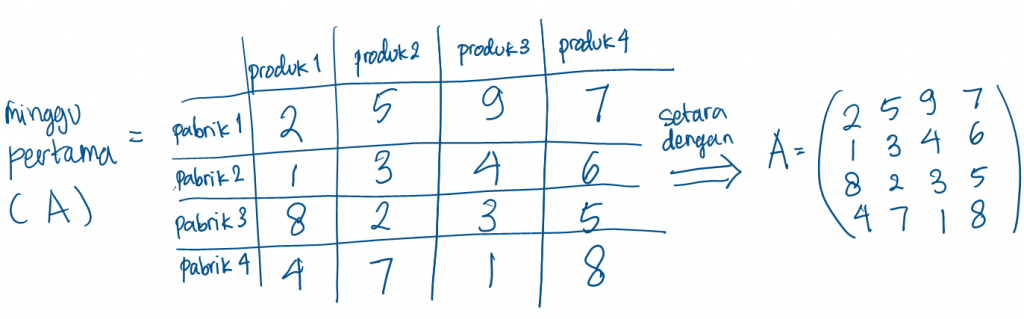
Apakah angka-angka dalam matriks hanyalah angka-angka acak? Tentu saja, tidak! Mari beri arti dalam angka-angka tersebut. Anggap kita dirikan bersama sebuah perusahaan bernama MAKMUR SENTOSA mempunyai 4 pabrik dan 4 produk. Kolom matriks A merepresentasikan produk, baris merepresentasikan pabrik, dan komponen angka adalah jumlah barang yang diproduksi dari sebuah pabrik di sebuah produk dalam satu minggu (satuannya misalkan 1000 buah).
Pada minggu yang lain, jumlah barang direpresentasikan oleh matriks B. Bagaimana kita bisa mengetahui jumlah barang di kedua minggu tersebut? Jawabannya ialah seperti di gambar sebelumnya ketika kita menjumlahkan dua matriks A dan B.
Apakah akan sama apabila dua matriks dikalikan? Mari kita lihat contoh berikutnya. Kita ingin mengetahui total keuntungan yang bisa didapatkan dan volume yang harus disiapkan untuk menyimpan barang-barang tersebut. Keuntungan per barang (satuannya misalnya 10000 rupiah) dan volume per barang (satuannya misalnya 10 m3) bisa direpresentasikan dalam matriks C dan dengan mudahnya kita tinggal mengalikan matriks hasil penjumlahan matriks A dan B dengan C.
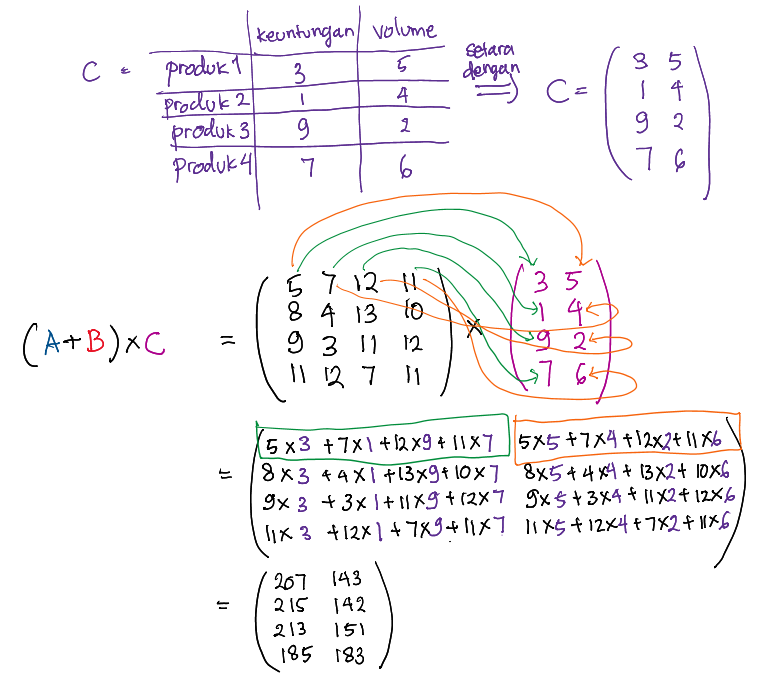
Apakah teman-teman bisa melihat pola dalam perkalian dari gambar di atas? Hasil akhir matriks akan mempunyai ukuran 4 x 2 atau 4 baris 2 kolom. Pada posisi kolom 1 baris 1, hasil dari penjumlahan angka hasil dari perkalian di posisi kolom 1 baris 1 matriks A kolom 1 baris 1 B, kolom 2 baris 1 matriks A kolom 1 baris 2 matriks B, dan seterusnya seperti yang ditunjukkan oleh warna hijau, demikian juga untuk kolom selanjutnya (warna oranye). Dilanjutkan dengan inspeksi baris 2 dari matriks A, akan membuahkan komponen hasil di posisi baris 2.
Untuk lebih mudah mengingat, kesimpulannya adalah perkalian dalam matriks terjadi dengan mengalikan satu baris matriks yang pertama disebut dengan satu kolom matriks selanjutnya. Karena proses perkalian seperti inilah, jumlah kolom matriks pertama harus sama dengan jumlah baris matriks kedua.

Selain ukuran matriks, urutan matriks dalam sebuah perkalian juga penting dan memengaruhi hasil. Kita bisa coba dengan cara mengalikan matriks B dengan matriks A (B×A) dan juga sebaliknya dengan menggunakan contoh terakhir di gambar yang mempunyai ukuran yang pas untuk 2 operasi tersebut. Apakah hasilnya sama?
Perbedaan lainnya aljabar luar biasa dibandingkan aljabar biasa adalah inversnya yang tidak biasa. Invers dari a = 8 adalah 1/8. Nah, apa sih yang ekuivalen dengan 1 di aljabar luar biasa? Biasanya disebut sebagai matriks identitas adalah matriks dengan ukuran yang sama dengan sebuah matriks, tetapi diagonalnya berisi angka satu. Apabila sebuah matriks dikalikan dengan inversnya, matriks identitas dapat dihasilkan.

Sekian dahulu sedikit tentang perbedaan aljabar “b aja” dengan aljabar luar biasa. Kita tidak perlu takut apabila data kita ratusan, ribuan atau jutaan, karena komputer bisa kalkulasikan sebanyak apapun (tentunya dengan limitasi seberapa kuatnya komputer tersebut ?). Yang penting kita ingat adalah konsep dasar dan perbedaan dari aljabar biasa yang lebih umum, seperti dicontohkan dalam artikel ini.
Bahan bacaan:
Crilly, T. “50 Mathematics ideas you really need to know.” London: Quercus (2007).
Penulis:
Kinanti Hantiyana Aliyah, Mahasiswa S3, ETH Zurich & Paul Scherer Institute, Swiss.



