Ketika teman-teman diperintahkan untuk menggambar sebuah benda, katakanlah sebuah vas bunga di kertas dengan mudah pasti teman-teman dapat menggambar lekukan-lekukan atau kurva yang membentuk vas bunga tersebut. Nah, sekarang coba bayangkan ketika teman-teman diperintahkan untuk menggambar vas bunga yang sama di komputer menggunakan sebuah perangkat lunak (software).
Untuk menggambar kurva dengan perangkat lunak di komputer, kita bisa memanfaatkan peralatan pembuat kurva di program tersebut. Sebagai contoh, dalam program Paint, kita bisa memilih “Curve Tool”, lalu tekan dan tarik (click & drag) untuk membuat sebuah garis, dan terakhir kita bisa menekan di tempat lain untuk membuat sebuah kurva. Nah, tahukah teman-teman bagaimana proses pembuatan kurva tersebut?
Kurva tersebut dinamakan kurva Bezier (Bezier Curve) yang dipopulerkan oleh Pierre Bezier, seorang insinyur yang bekerja di perusahaan otomotif Renault di Perancis. Sebelum masuk lebih lanjut untuk mengenal kurva Bezier, mari kita kunjungi dulu persamaan garis.
Persamaan garis
Mungkin teman-teman masih ingat dengan persamaan garis yang diajarkan di SMP dulu. Persamaan garis dapat dituliskan sebagai berikut:
$latex y = mx + c$
Dalam persamaan tersebut, y merupakan koordinat y, x merupakan koordinat x, m merupakan gradien (kemiringan) garis, dan c merupakan nilai konstan.
Ketika kita mengetahui nilai m dan c, lalu diberikan nilai x, dengan mudah kita dapat menghitung nilai y. Jadi, y merupakan variabel yang bergantung terhadap nilai x yang merupakan variable independen.
Tahukah teman-teman bahwa persamaan tersebut dapat direpresentasikan ke dalam bentuk yang lain? Berikut ini merupakan bentuk lain dari persamaan garis:
$latex \binom{x}{y}=\binom{x_0}{y_0}+t\binom{v_x}{v_y}$
Persamaan di atas dapat dianalogikan sebagai berikut. Anggaplah kita sedang berdiri di suatu posisi $latex \left(x_0,\\ y_0 \right )$ dan kita ingin bergerak ke posisi lain $latex \left ( x, \\ y \right )$ yang arahnya ditentukan oleh vektor posisi $latex \bar{v} \left (v_x, \\ v_y \right )$ . Sebanyak apa kita harus melangkah? Jawabannya adalah sebanyak t langkah.
Nah, pertanyaannya, variabel apakah dari persamaan garis baru di atas yang merupakan variabel independen? Jawabannya adalah variabel t. Bentuk semacam ini, ketika dua persamaan (atau lebih) dapat direpresentasikan dengan sebuah variabel independen, dinamakan sebagai bentuk parametrik.
Ibarat beli barang, bentuk parametrik bisa dikatakan: beli satu dapat dua! Masukkan satu variabel t, kita mendapatkan dua nilai, masing-masing untuk x dan y. Nah, setelah kita tahu bentuk parametrik untuk persamaan garis, saatnya kita masuk ke acara utama untuk artikel ini, kurva Bezier!
Kurva Bezier
Sebuah kurva Bezier ditentukan dari posisi titik-titik kontrolnya (control points). Jumlah dari titik kontrol (n + 1) sebuah kurva Bezier akan menentukan pula orde (n) dari kurva tersebut. Sebagai contoh, sebuah kurva dengan tiga titik kontrol merupakan kurva dengan orde 2. Besarnya orde menentukan seberapa kompleksnya sebuah kurva dibentuk. Perhatikan contoh dari kurva Bezier berorde 2 dan 3.
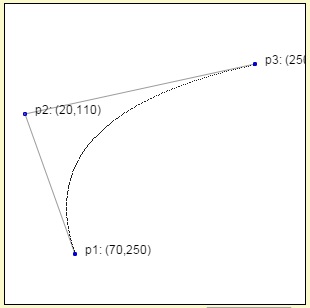
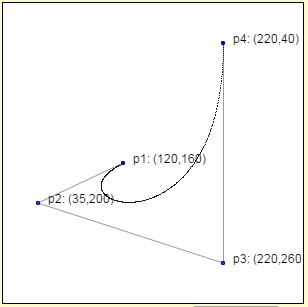
Kurva Bezier memiliki persamaan umum sebagai berikut:
$latex B(t) = \sum_{i=1}^{n} b_i B_{i,n} (t)$
$latex B_{i,n} (t) = \begin{cases} \frac{n!}{(n-i)! i!} (1-t)^{n-i} t^{i}& {\rm jika}\ 0\leq i \leq n \\ 0& {\rm lainnya} \end{cases}$
Pada persamaan umum kurva Bezier, $latex b_i$ merupakan titik kontrol dari kurva Bezier dan variabel n merupakan jumlah titik kontrol kurva Bezier. Mungkin beberapa dari teman-teman ada yang berpikir, “Hmm… rasanya tadi sudah lihat variabel t ini deh.” Tepat sekali! Variabel t ini sama dengan t yang kita bahas sebelumnya di persamaan garis.
Jadi, sebenarnya kurva Bezier merupakan sebuah persamaan parametrik untuk kurva. Perlu diperhatikan bahwa nilai t di persamaan umum kurva Bezier mempunyai selang $latex 0 \leq t \leq 1$ . Nilai t = 0 artinya dimulai dari titik pertama dan t = 1 artinya kita telah sampai di titik terakhir.
Lalu, apa itu Bi,n(t)? Bi,n(t) seringkali disebut dengan polinomial Bernstein (Bernstein polynomial). Polinomial Berstein inilah yang memberikan efek atau kekuatan untuk setiap titik di setiap t. Lebih jelasnya, mari kita lihat contoh persamaan untuk kurva kuadratik sebagai berikut:
$latex B(t) = (1-t)^{2} b_o + 2t(1-t)b_1 + t^{2} b_2$
Untuk yang penasaran, boleh juga coba turunkan persamaan kurva kuadratik di atas dari persamaan umum Bezier.
Bila setiap fungsi polinomial Bernstein kita plot, dapat dihasilkan tiga kurva seperti pada gambar.
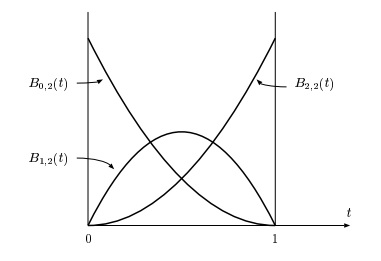
Apa maksudnya plot polinomial Bernstein tersebut? Dari plot tersebut, kita bisa lihat “kekuatan” dari masing-masing titik untuk nilai t tertentu.
B0,2 merupakan kurva (1 – t)2, B1,2 merupakan kurva untuk 2t(1 – t), dan B2,2 merupakan kurva untuk t2. Untuk nilai t = 0, B0,2 memiliki kekuatan yang paling besar dan yang lainnya memiliki nilai 0. Untuk nilai t = 0,5, kita bisa lihat bahwa kurva B0,2 dan kurva B2,2 memiliki nilai yang sama (perpotongan antara kurva di tengah-tengah), sedangkan kurva B1,2 memiliki nilai yang lebih tinggi dari dua kurva yang lain. Artinya, titik ke-2 memiliki kekuatan yang lebih besar untuk “menarik” kurva ke posisinya.
Nah, sekarang teman-teman sudah tahu bagaimana kurva dibentuk. Sebenarnya masih banyak tipe kurva lain dan pengembangan dari kurva-kurva Bezier seperti Piecewise Bezier Curve (gabungan dari beberapa kurva Bezier), B-Spline Curve, dan NURBs. Kurva-kurva lainnya tidak akan dibahas di sini. Untuk teman-teman yang tertarik bisa mencari informasi-informasi mengenai kurva-kurva di atas secara pribadi di internet atau buku-buku yang ada. Siapa tahu suatu saat nanti teman-teman bisa membuat persamaan kurva unik milik teman-teman sendiri.
Bahan bacaan:
- http://pomax.github.io/bezierinfo/
- http://www.mactech.com/articles/develop/issue_25/schneider.html
- Marsh, Duncan. 2005. Applied Geometry for Computer Graphics and CAD. Springer-Verlag, London.
Penulis:
Vicky Sintunata, mahasiswa doktor di Graduate School of Information Science, Tohoku University, Jepang.
Kontak: vicky_sintunata(at)yahoo.co.id



