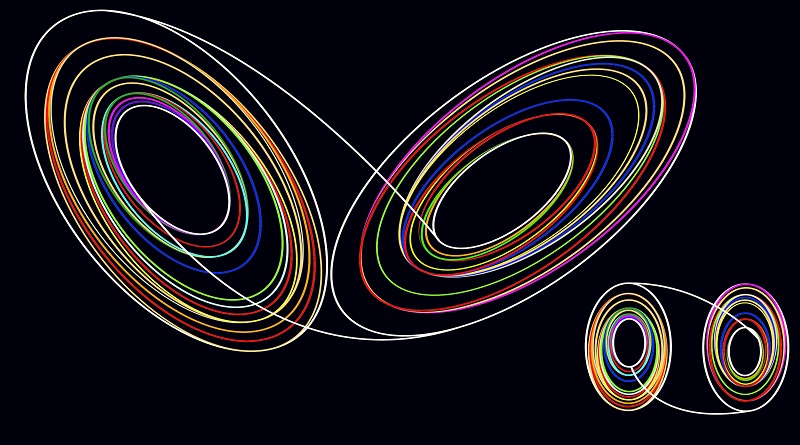Teori Kekacauan (Chaos Theory)

Bagaimanakah kita dapat menggambarkan atau memformulasikan kekacauan dalam bentuk sebuah teori? Bukankah kekacauan muncul karena ketiadaan teori? Cerita ini bermula di tahun 1812. Kala itu Napoleon sedang menyerang Moskow. Temannya yang bernama Simon de Laplace memublikasikan sebuah esai tentang alam semesta yang deterministik (dapat ditentukan keadaannya di masa depan bila segala parameter di masa sekarang diketahui).

Laplace berpendapat apabila posisi dan kecepatan dari semua objek di alam semesta diketahui pada suatu waktu, kemudian gaya yang bekerja padanya juga diketahui, maka posisi dan kecepatan pada masa datang dapat diketahui. Dengan demikian alam semesta dan semua objek dapat sepenuhnya diketahui (deterministik). Namun, teori kekacauan menyebutkan bahwa alam semesta lebih rumit daripada sekadar deterministik. Kenyataannya kita tidak dapat mengetahui posisi, kecepatan dan gaya semua objek alam semesta secara eksak. Anggaplah kita dapat mengestimasi besarnya besaran-besaran tersebut dengan pengetahuan yang kita miliki, tetap saja memprediksi besaran fisis di masa mendatang tidaklah mudah.

Mungkin kita bisa berimajinasi bahwa pelari yang mulai berlari 1/10 detik setelah tanda senapan dibunyikan akan sampai 1/10 detik lebih lambat di garis finis daripada waktu rata-ratanya. Sedikit perubahan di keadaan awal akan mengubah sedikit keadaan akhir. Akan tetapi, bagaimana jika ada kasus dengan sedikit perubahan di keadaan awal akan memengaruhi perubahan yang drastik di akhir? Itulah yang akan kita bahas dalam teori kekacauan.

Efek kupu-kupu (Butterfly effect)

Efek kupu-kupu menunjukkan bagaimana perubahan yang sangat kecil dapat membangkitkan keluaran yang berbeda sangat jauh dari yang diharapkan. Ibaratnya, kepakan seekor kupu-kupu memengaruhi rapat-renggang udara sehingga mengubah cuaca di suatu belahan bumi. Tentu saja contoh tersebut sangat dibesar-besarkan, tetapi kita akan melihat bahwa efek ini nyata dari contoh-contoh berikut ini.

Bean machine

Bean machine adalah suatu permainan yang terdiri atas kelereng dan paku atau pin yang tersusun seperti piramid seperti gambar di bawah.

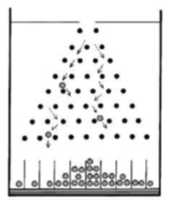
Bayangkan Anda memegang kelereng tersebut dan kemudian menjatuhkannya, pada langkah pertama mungkin kelereng akan berbelok ke kanan, lurus dan kemudian ke kiri, hingga akhirnya masuk ke salah satu kantong. Dengan sangat hati-hati Anda mencoba untuk mengulangi dengan posisi dan kecepatan yang sama. Akan tetapi, probabilitas seluruh gerakan berulang hingga akhirnya jatuh di kantong yang sama adalah sangat kecil atau hampir mustahil.

Sedikit saja perbedaan sentuhan akan memberikan luaran yang jauh berbeda dari kejadian sebelumnya. Namun, bean machine ini memenuhi sifat statistik, yakni ketika kelereng dilepaskan secara acak dalam jumlah banyak akan memunculkan distribusi normal berbentuk fungsi Gauss. Ini merupakan suatu kekacauan, tetapi pada derajat tertentu bersifat deterministik.

Bandul

Bandul dengan satu pemberat relatif stabil. Misalkan kita simpangkan bandul dari titik setimbangnya dengan simpangan cukup besar, simpangan bandul lama kelamaan akan mengecil. Kita dapat menggambarkan hubungan posisi dengan kelajuan bandul.

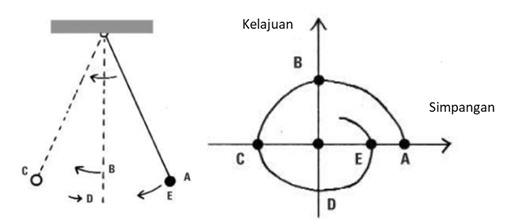
Saat simpangan maksimum di A, kelajuan bandul nol. Tergambar di panel kanan posisi A dengan simpangan (sumbu x) maksimum dan kelajuan (sumbu y) nol. Pada titik B, simpangan bernilai nol sementara kelajuan maksimum sehingga A dan B terhubung oleh garis lengkung. Demikian seterusnya hingga bandul kembali ke simpangan sebelumnya di E dengan simpangan lebih kecil karena efek gesekan udara.

Plot simpangan terhadap kelajuan akan berbentuk spiral yang makin lama makin kecil hingga berakhir di (0,0) dengan simpangan dan kelajuan yang bernilai nol. Akan tetapi, hasil ini akan jauh berbeda bila kita menggunakan bandul dengan dua pemberat.

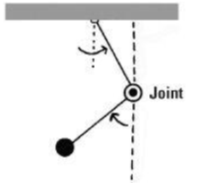
Bila kita gerakkan dengan simpangan kecil, kurang lebih hasilnya akan sama dengan satu bandul. Namun, pada simpangan besar, pergerakan bandul akan makin kompleks. Pergerakan bandul atas dan bawah saling memengaruhi dan tidak mungkin kita memiliki kurva spiral hubungan kelajuan dan simpangan seperti gambar sebelumnya. Perbedaan yang kecil pada kondisi awal akan memberikan hasil akhir yang berbeda besar.

Model pertumbuhan populasi

Contoh terakhir adalah suatu model pertumbuhan populasi. Kita definisikan suatu populasi kelinci pada tahun ke n adalah x_n, dengan x_n bernilai dari 0 hingga 1. Pertumbuhan populasi kelinci adalah sebesar r. Maka,  pada tahun beikutnya populasi kelinci dapat dituliskan dengan suatu model seperti berikut

x_n+1 = x_n r (1- x_n)

Ketiadaan faktor (1 – x_n)   membuat x_n+1 terus-menerus bertambah tak berhingga pada waktu yang lama. Faktor (1 – x_n) menstabilkan persamaan. Contoh kasusnya, misalkan kita mulai dengan x₁ = 0.4 dan melihat dua nilai r lebih besar dan lebih kecil dari 1 seperti pada kurva di gambar.

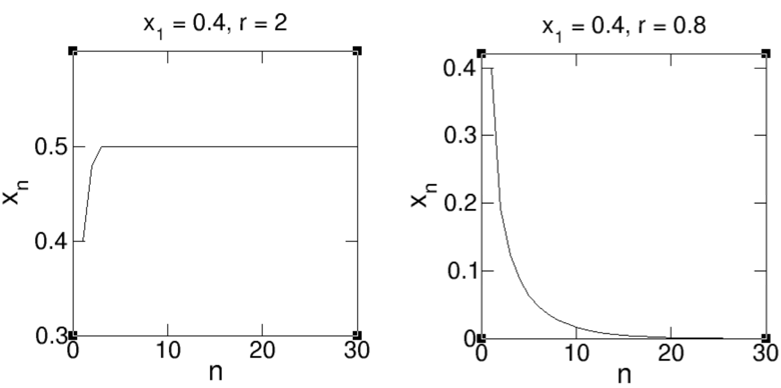
Pada saat r > 1, nilai x_n mula-mula naik secara monoton hingga akhirnya stabil di angka 0.5. Dengan r  < 1, populasi kelinci berkurang sepanjang tahun sehingga mengecil dan akhirnya punah. Hasil menarik akan kita dapat bila kita perbesar nilai r hingga 3.8. Pada nilai ini x_n tidak dapat menjadi stabil. Kita coba membuat plot x_n pada kisaran n mendekati 100 sebagai fungsi r dan melihat ada di mana nilai x_n yang mulai tidak stabil.

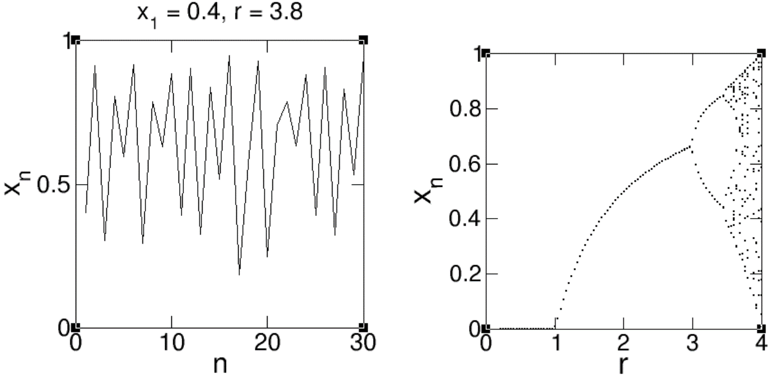
Pada gambar di kanan, kita melihat bahwa x_n bercabang dua saat nilai r di kisaran 3. Setelah itu, setiap cabangnya membentuk dua cabang lagi, dan seterusnya. Pola percabangan ini merupakan suatu fraktal  yang berkaitan dengan himpunan Mandelbrot.

Cukup menarik melihat suatu bentuk kekacauan tetapi di sisi lain terdapat pola simetri fraktal. Pelajaran bagi kita, tidak selalu yang tidak teratur itu tidak memiliki pola dan tidak semua yang memiliki pola teratur. Mungkin itulah seni kehidupan.

Bahan bacaan:

• Tony Crilly, “50 Mathematical ideas you really need to know” (Bertram Books, 2007).
• “This equation will change how you see the world”: https://youtu.be/ovJcsL7vyrk
• “Normal Distribution Demonstration”: https://youtu.be/PM7z_03o_kk
• http://majalah1000guru.net/2018/06/fisika-nonlinear/
• http://majalah1000guru.net/2013/10/matematika-dan-seni/
• http://majalah1000guru.net/2012/01/berkenalan-dengan-fraktal/

Penulis:
Eddwi Hesky Hasdeo, Peneliti di Pusat Penelitian Fisika, Lembaga Ilmu Pengetahuan Indonesia.
Kontak: heskyzone(at)gmail(dot)com