Dilema bilangan imajiner terjadi ketika kita menyelesaikan persamaan kuadrat. Kita ambil contoh suatu fungsi kuadrat, f(x) = x^2 + 1 , kemudian kita bertanya berapakah akar-akar dari fungsi tersebut, atau dalam kata lain berapakah nilai x yang membuat f(x) bernilai nol. Salah satu cara mencari akar-akar suatu fungsi adalah dengan menggambarnya.
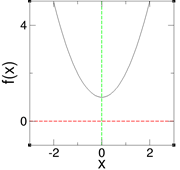
Kita melihat bahwa plot f(x) = x^2 + 1 selalu berada di atas garis, yaitu garis merah pada sumbu x sehingga dapat disimpulkan bahwa f(x) tidak mempunyai akar. Akan tetapi, seorang matematikawan jenius Carl F. Gauss menyatakan dalam dasar teorema aljabar bahwa setiap polinomial ber-orde n haruslah memiliki n akar. Teorema dasar aljabar ini bertentangan dengan hasil yang kita dapat di atas bahwa seharusnya f(x) memiliki dua akar yang membuat nilai f(x) bernilai nol.
Tentu saja bila kita menyelesaikan persamaan x^2 + 1 = 0 , kita akan mendapatkan x = \pm\sqrt{-1} = \pm i dengan i = \sqrt{-1} yang kemudian kita kenal sebagai bilangan imajiner. Hmm… tetapi, bagaimana kita dapat membuktikannya dengan gambar bahwa f(x) benar-benar dapat melewati garis merah sumbu x?
Permasalahan ini muncul karena dalam plot itu kita hanya membatasi bilangan kita di dalam sumbu x atau sumbu bilangan riil saja. Kita sebentar lagi akan melihat bahwa f(x) benar-benar melewati nol bila kita menambahkan dimensi bilangan.
Bila f(x) positif kita plot ke atas, dan sumbu-x positif kita plot ke kanan, kini kita menambahkan sumbu bilangan imajiner ke depan (keluar dari kertas menuju mata kita). Hasilnya seperti pada gambar tiga dimensi. Jelaslah bahwa selama ini kita tidak melihat kurva f(x) seutuhnya karena kita hanya melihat dalam dimensi bilangan riil saja.

Penamaan bilangan imajiner sebenarnya merupakan kontroversi yang membuat kita beranggapan bahwa bilangan ini tidak nyata dan hanya ada di dalam imajinasi kita untuk memecahkan permasalahan matematika. Gauss pun menolak penamaan bilangan imajiner. Beliau berkata, “If we call +1, -1, and √-1 had been called direct, inverse and lateral units, instead of positive, negative, and imaginary (or impossible) units, such an obscurity would have been out of the question.”
Gauss lebih suka menyebut bilangan imajiner sebagai bilangan lateral, yaitu bilangan yang berada di dalam dimensi lain yang tegak lurus dengan bilangan natural. Tapi apa boleh dikata, para matematikawan telah menyepakati penyebutan bilangan riil dan imajiner bukan bilangan natural dan lateral.
Kini kita mengetahui bahwa bilangan tidak tinggal di satu dimensi (bilangan riil) saja, tetapi di dua dimensi (riil dan imajiner) yang kita sebut bilangan kompleks. Dengan memiliki perspektif yang lebih luas seperti itu, berbagai permasalahan dalam matematika, fisika, dan teknik dapat lebih mudah diselesaikan. Suatu saat di majalah 1000guru kita akan bahas aplikasi bilangan kompleks untuk mempermudah perhitungan matematis.
Bahan bacaan:
- Imaginary numbers are real. http://www.welchlabs.com
Penulis:
Eddwi Hesky Hasdeo, Peneliti Fisika di Lembaga Ilmu Pengetahuan Indonesia.
Kontak: heskyzone(at)gmail.com



