Di kelas matematika, Pak Mate mengajarkan pada anak-anak tentang bagaimana menggambar grafik fungsi linear dan kuadratik. Tika dalam hati menggerutu, “Saya tidak punya bakat menggambar grafik fungsi. Sulit bagiku untuk mengimajinasikan suatu persamaan ke dalam grafik.” Sebelum penjelasan tentang menggambar grafik dimulai, Pak Mate berjanji bahwa menggambar grafik akan mudah dan menyenangkan. Mari kita ikuti penjelasannya.
Fungsi Linear
Bagi sebagian orang, tidak mudah untuk menggambar grafik fungsi linear. Misalkan menggambar fungsi y = 3x + 1. Untuk menggambar fungsi tersebut, kita bisa lakukan dua langkah berikut ini.
- Gambar fungsi y1 = 3x
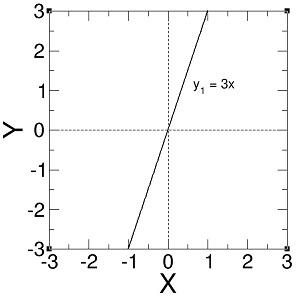
Perhatikan bahwa gradien fungsi y1 adalah 3. Saat nilai x meningkat 1 unit, nilai y1 meningkat 3 unit. Fungsi y1 tidak memiliki konstanta sehingga garis y1 melewati titik koordinat (0, 0).
- Gambar fungsiy = 3x + 1 = y1 + 1
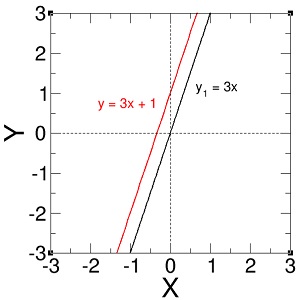
Setelah menggambar grafik fungsi y1, grafik fungsi y = 3x + 1 didapatkan dengan menggeser garis y1 sebesar 1 unit ke atas.
Sekarang bagaimana kalau permasalahan kita balik. Dengan diberikan grafik, kita harus menebak bagaimana bentuk fungsi tersebut.
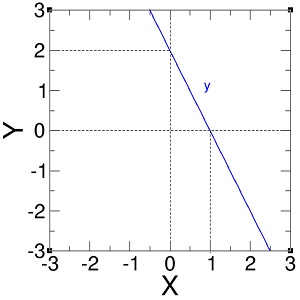
Banyak metode untuk menentukan bentuk fungsi linear suatu garis. Kali ini kita akan menentukan bentuk fungsi linear hanya dengan sebuah metode yang berlaku umum untuk semua permasalahan, yaitu substitusi dua titik ke dalam fungsi umum
y = mx + c, …(1)
m dan c adalah nilai-nilai yang harus kita cari dengan memasukkan dua titik koordinat (x,y) ke dalam persamaan di atas.
Untuk mengetahui bentuk fungsi suatu garis linear, minimal kita membutuhkan 2 titik. Dari grafik di pada gambar, kita mendapati bahwa garis y melewati 2 titik di koordinat (1, 0) dan (0, 2). Dengan memasukkan koordinat (1, 0) ke dalam persamaan (1), kita mendapatkan
0 = m + c, …(2)
dan dengan memasukkan koordinat (0, 2) ke persamaan (1), kita mendapatkan
2 = c. …(3)
Substitusikan kembali hasil dari persamaan (3) ke persamaan (2), kita mendapatkan nilai m = –2. Maka, fungsi yang diperoleh adalah y = –2x + 2 yang ditunjukkan pada gambar. Gradien m bernilai negatif yang mengindikasikan bahwa nilai y semakin turun saat x meningkat.
Fungsi Kuadratik
Selanjutnya kita akan naik ke level yang lebih tinggi, yakni menggambar grafik fungsi kuadratik. Bentuk umum fungsi kuadratik adalah
y = ax2 + bx + c, …(4)
dengan a, b, dan c berturut-turut adalah koefisien kuadrat, koefisien linear, dan konstanta. Menggambar bentuk fungsi dengan nilai a, b, dan c tidak nol itu cukup rumit. Mari kita mulai dengan permasalahan yang lebih mudah, yaitu saat salah satu nilai b atau c adalah nol.
Kita mulai dengan menggambarkan fungsi dengan bernilai nol, sebagai berikut:
y = ½x2 – 2. …(5)
Pertama-tama kita menggambar fungsi y1 = ½x2.
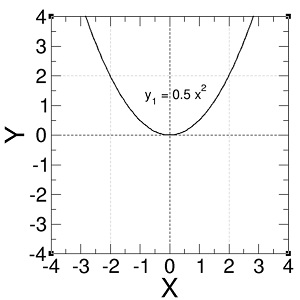
Kemudian, kita geser y1 ke bawah sebanyak dua unit untuk mendapatkan fungsi y = ½x2 – 2.
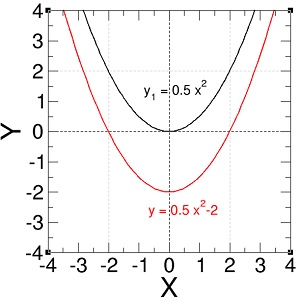
Sekarang kita coba gambar fungsi kuadratik dengan c bernilai nol sebagai berikut:
y = –½x2 + x. …(5)
Langkah pertama untuk menggambar fungsi di atas adalah dengan melakukan faktorisasi. Persamaan (5) dapat dituliskan menjadi
y = –½x (x – 2). …(6)
Dari hasil faktorisasi, kita dapat memperkirakan bahwa y bernilai nol saat x = 0 dan x = 2. Kemudian, kita masukkan satu nilai acak misalnya x = 1 mendapatkan nilai y = ½. Jadi, kita tahu bahwa y melewati titik-titik koordinat (0, 0), (0, 2), dan (1, ½). Dengan menghubungkan ketiga titik tersebut kita akan mendapatkan grafik fungsi kuadratik yang diinginkan. Perhatikan bahwa saat nilai a negatif, fungsi y memiliki titik maksimum, sedangkan saat a positif, fungsi y memiliki titik minimum.
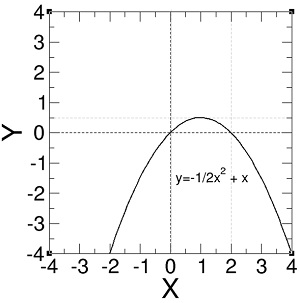
Kini dengan persoalan yang lebih sulit, misalnya menggambarkan fungsi y2 = –½x2 + x + 1, kita cukup menggeser fungsi y satu unit ke atas untuk mendapatkan grafik yang diinginkan.
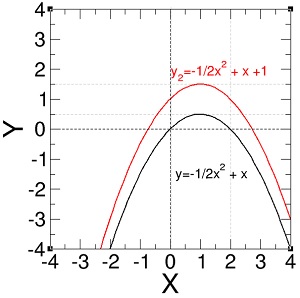
Selanjutnya, kalau kita harus menentukan bentuk suatu fungsi kuadratik dari sebuah grafik, kita perlu kembali gunakan persamaan umum
y = ax2 + bx + c.
Dari sini kita tentukan nilai a, b, dan c untuk tiga titik koordinat yang didapatkan dari grafik.
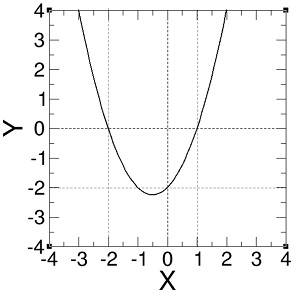
Pertanyaan: Apa fungsi matematis dari kurva fungsi kuadratik pada gambar?
Misalkan kita memiliki suatu kurva yang belum diketahui bentuk fungsinya seperti pada gambar. Dari grafik di atas, kita tahu fungsi y melewati titik-titik (–2, 0), (1, 0), dan (0, –2). Kita masukkan nilai-nilai x dan y dari koordinat tersebut ke persamaan umum fungsi kuadratik sehingga
0 = a (–2)2 + b (–2) + c, …(7)
0 = a (1)2 + b (1) + c, …(8)
–2 = c. …(9)
Dengan menyelesaikan persamaan-persamaan (7)-(9) melalui metode substitusi atau eliminasi, kita mendapatkan nilai a = 1, b = 1, dan c = –2 sehingga fungsi kuadratiknya bisa ditulis secara lengkap:
y = x2 + x – 2.
Kembali ke cerita di awal, setelah mendapatkan penjelasan dari Pak Mate, sekarang Tika menjadi bersemangat dalam menggambar grafik persamaan linear dan kuadratik. Di akhir kelasnya, Pak Mate memberikan sebuah tantangan, “Gambarkan suatu fungsi kuadratik y = ax2 + bx + c dengan nilai-nilai a, b, dan c berturut-turut adalah merupakan deret geometri 1, 2, 4, 8, 16, …”
Apakah teman-teman dapat melihat suatu hasil yang menarik dari grafik-grafik yang teman-teman gambar? Bagaimana jika deret geometri diganti dengan deret pecahan 1, 1/2, 1/4, 1/8, 1/16, …? Apakah ada perbedaan grafik fungsi kuadratik dengan gambar sebelumnya?
Selamat mencoba!
Penulis:
Eddwi Hesky Hasdeo, Mahasiswa S3 Jurusan Fisika Tohoku University.
Kontak: heskyzone(at)gmail(dot)com



