Sekitar bulan Juni 2006, Sir John M. Ball, presiden International Mathematical Union (IMU), mengunjungi Rusia untuk bertemu seorang matematikawan, Grigori Perelman. Kehadirannya ke Rusia semata untuk membujuk Perelman supaya dia mau menerima Fields Medal, penghargaan bergengsi setara dengan hadiah Nobel untuk bidang matematika.
Selama dua hari mereka berbincang sambil ditemani kopi dan jalan kaki bersama melintasi kota St. Petersburg, tetapi usaha Ball untuk membujuk Perelman berbuah nihil. Perelman menolak dengan berkata, “I’m not interested in money or fame. I don’t want to be on display like an animal in a zoo. I’m not a hero of mathematics. I’m not even that successful; that is why I don’t want to have everybody looking at me.” Dia tidak hanya menolak medali tersebut, tetapi juga menolak hadiah uang satu juta dolar dari IMU.

Kita tidak akan membahas lebih lanjut alasan mengapa Perelman menolak Fields Medal, tetapi kita akan fokus dengan pertanyaan, “Apa yang telah dicapai Perelman sehingga dia sangat dihormati oleh para komunitas matematika Internasional dan layak mendapatkan Fields Medal?” Jawabannya adalah karena dia berhasil membuktikan dugaan Poincare (Poincare’s conjecture). Sebelum kita belajar tentang dugaan Poincare, sebaiknya kita bermain dahulu dengan zat malam atau lilin (clay) yang sering kita mainkan sewaktu kecil.

Kita dapat membentuk malam ini menjadi sebuah bola, kubus, piramid dan bentuk apapun yang kita suka. Dalam ilmu geometri, kita tahu bahwa kubus, piramid, maupun bola adalah entitas yang berbeda. Namun, dalam ilmu topologi, mereka semua dapat ditekan, ditarik, dan dibentuk sedemikian rupa hingga menjadi bentuk yang paling sederhana, yaitu bola. Bila kita membuat simpul melalui diameter bola kemudian menarik simpul itu, tali dengan mudah meninggalkan bola itu dan membentuk simpul dengan dirinya sendiri. Sifat simpul ini berlaku sama untuk kubus, piramid, dan bola.

Lain halnya jika kita memiliki suatu bentuk yang berlubang seperti donat. Jika kita memasukkan tali ke dalam lubang donat kemudian membentuk simpul, simpul tali tidak akan dapat meninggalkan donat.

Dalam topologi, bola atau apapun struktur tak berlubang yang dapat dibentuk menjadi bola bersifat tersambung sederhana (simply connected). Sementara itu, donat bersifat tak tersambung sederhana karena ada lubang di tengahnya. Bola tidak dapat diubah menjadi donat ataupun sebaliknya donat tidak dapat diubah menjadi bola tanpa harus merobek atau melubangi permukaannya. Nah, yang menarik, dalam matematika, cangkir justru dapat diubah menjadi donat seperti gambar di bawah ini. Dengan kata lain, donat memiliki topologi yang berbeda dengan bola, tetapi donat memiliki topologi yang sama dengan cangkir.

Setelah memahami sedikit tentang ilustrasi topologi ini, kita kembali ke pertanyaan awal, apa yang dimaksud dengan “dugaan Poincare”? Pada tahun 1900, matematikawan Perancis Henri Poincare mengungkapkan bahwa di dalam dunia empat dimensi, segala hal yang terhubung sederhana, atau tidak memiliki lubang, dapat dibentuk menjadi bola empat dimensi.
Tentu sangat mudah untuk memahami bentuk bola dalam tiga dimensi. Dalam dua dimensi, kita juga dapat memahaminya sebagai lingkaran. Akan tetapi, kita mengalami kesulitan memahami bagaimana bentuk sebuah bola empat dimensi. Keterbatasan kita dalam memahami objek dengan dimensi lebih dari tiga membuat dugaan Poincare ini sangat sulit dibuktikan.
Pada tahun 2002, Grigori Perelman menulis tiga buah artikel yang membuktikan dugaan Poincare. Perelman melanjutkan pekerjaan Richard Hamilton tahun 1981 tentang aliran Ricci (Ricci flow). Aliran Ricci adalah suatu teknik dalam geometri diferensial yang juga dipakai dalam persamaan kalor. Kalor terdistribusi di dalam suatu ruang, mengalir dari tempat yang lebih panas ke tempat yang lebih dingin sehingga membuat suhu yang lebih seragam. Demikian pula bila konsep aliran Ricci diterapkan dalam topologi, kita dapat mengalirkan “kalor” (mengubah permukaan benda) untuk menyeragamkan kelengkungan benda tersebut sehingga menjadi bola.
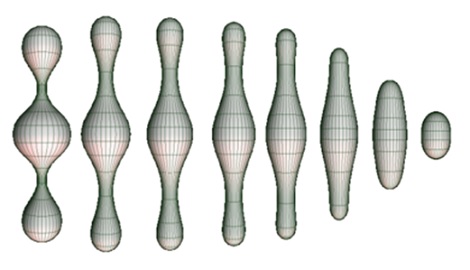
Cukup sederhana bila kita pahami di dunia tiga dimensi, tetapi tidak mudah untuk membahasnya di dunia dengan dimensi lebih dari tiga.
Bahan bacaan:
- https://medium.com/@phacks/how-grigori-perelman-solved-one-of-maths-greatest-mystery-89426275cb7
- http://www.newyorker.com/magazine/2006/08/28/manifold-destiny
- https://www.youtube.com/watch?v=TzMZKiCgEVE
- https://en.wikipedia.org/wiki/Grigori_Perelman
- Artikel Grigori Perelman yang membuktikan dugaan Poincare:
- Perelman, Grisha (November 11, 2002). “The entropy formula for the Ricci flow and its geometric applications”.arXiv:DG/0211159
- Perelman, Grisha (March 10, 2003). “Ricci flow with surgery on three manifolds”.arXiv:DG/0303109
- Perelman, Grisha (July 17, 2003). “Finite extinction time for the solutions to the Ricci flow on certain three-manifolds”.arXiv:DG/0307245
Penulis:
Eddwi Hesky Hasdeo, Mahasiswa S3 Jurusan Fisika Tohoku University.
Kontak: heskyzone(at)gmail(dot)com



