Di bawah ini ada dua gambar lukisan yang digantung pada dua buah paku dengan lilitan yang berbeda. Pertanyaannya, bila salah satu paku dicabut, lukisan mana yang akan tetap tergantung?
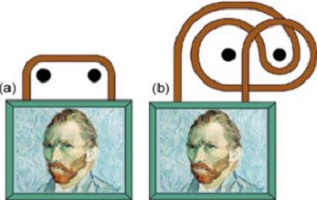
Bagaimana? Pasti mudah bagi teman-teman menjawab teka-teki ini. Untuk lukisan (a), bila salah satu paku dicabut, lukisan akan tetap tergantung. Untuk lukisan (b), jika salah satu paku dicabut, lukisan akan jatuh. Problem lukisan ini dikenal sebagai picture hanging puzzles. Nah, sekarang bagaimana untuk lukisan yang digantung dengan cara seperti di gambar berikutnya ini? Apa yang terjadi jika salah satu paku dicabut?
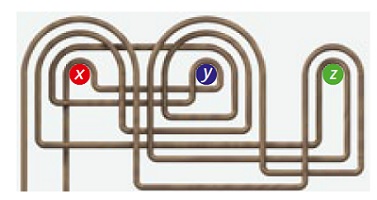
Untuk menyelesaikan dua teka-teki ini, ada satu teori matematika yang berguna dan membantu pemecahan masalah, yakni teori grup (group theory). Pertama-tama, kita tentukan elemen dari grup ini, yang disesuaikan dengan jumlah paku, x, y, z. Setiap elemen mempunyai lawannya atau invers yang kita tandai sebagai x’, y’, z’. Dalam teori grup, bila kita mengoperasikan suatu elemen dengan inversnya, hasilnya adalah 1. Sebagai contoh, xx’= x’x = 1. Elemen 1 disebut dengan elemen identitas.
Sekarang kita definisikan bahwa elemen grup berkaitan dengan arah lilitan dengan paku yang bersangkutan. Sebagai contoh, jika arah lilitan pada paku pertama searah jarum jam, arah lilitan itu adalah elemen x, sedangkan jika arah lilitan berlawan dengan arah jarum jam, kita bisa tandai sebagai inversnya, yaitu x’. Tetapi, ada satu aturan lagi dalam teori grup ini, yaitu perkalian antarelemen bersifat tidak komutatif. Sebagai contoh, xy’ tidak sama dengan y’x.
Dengan bantuan teori group, kita siap untuk menjawab teka-teki ini. Sebagai bahan latihan yang mudah, kita selesaikan teka-teki pertama bagian (b). Paku sebelah kiri adalah elemen x dan paku sebelah kanan adalah elemen y. Dengan menelusuri lilitan tali, maka lilitan pada lukisan b dapat dituliskan sebagai yxy’x’. Bila kita mencabut paku x, lilitan yang tersisa dapat ditulis sebagai yy’ = 1 (dengan menghilangkan elemen x dan inversnya). Berdasarkan hal ini, kita bisa katakan bahwa lukisan akan jatuh karena kita melilitkan tali pada paku y searah jarum jam dan melilitkan kembali pada arah berlawanan lagi.
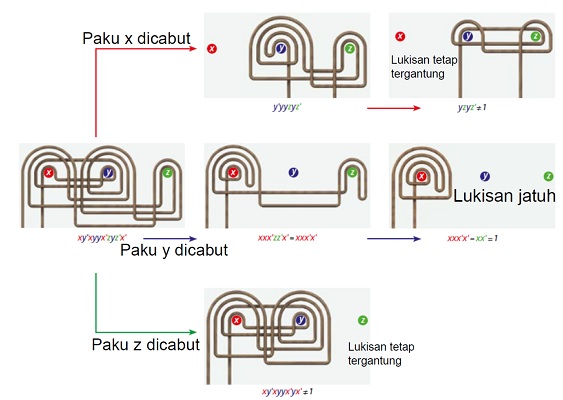
Selanjutnya kita coba selesaikan teka-teki kedua. Lilitan ini bisa dituliskan sebagai xy’xyyx’zyz’x’. Solusi diberikan pada gambar. Kita bisa lihat ternyata lukisan akan jatuh hanya jika paku y yang dicabut. Jika kita mencabut paku x ataupun paku z, lukisan tetap akan tergantung.
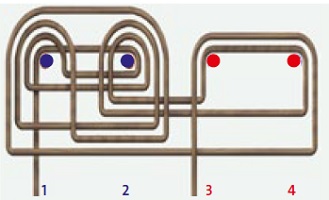
Nah, sekarang untuk latihan, kerjakan problem 1-4 pada teka-teki ketiga sesuai gambar. Tentukan paku apa saja yang harus dicabut, agar lukisan jatuh!
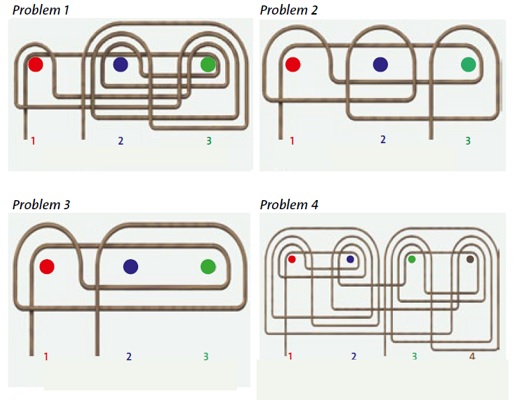
Jawaban dari teka-teki ketiga adalah:
- Lukisan jatuh jika salah satu dari ketiga paku dicabut.
- Lukisan jatuh jika dua dari ketiga paku (pilihan terserah) dicabut.
- Lukisan jatuh hanya jika paku 1 atau 2 dicabut bersamaan dengan paku 3.
- Lukisan jatuh jika salah satu paku dicabut.
Untuk lebih bersenang-senang dengan teori grup, silakan kerjakan teka-teki keempat seperti pada gambar. Tentukan paku apa saja yang harus dicabut, agar lukisan jatuh. Jawabannya pikirkan sendiri, ya!
Catatan:
Tulisan ini merupakan saduran bebas dari artikel berbahasa Jerman: Spektrum der Wissenschaft Magazin 02/02.2015: Die Tucken des Bilderaufhangens.
Bahan bacaan:
- http://arxiv.org/abs/1203.3602
- https://en.wikipedia.org/wiki/Group_theory
- http://mathworld.wolfram.com/Group.html
Penulis:
Muhammad Shoufie Ukhtary, mahasiswa doktor di Departemen Fisika, Tohoku University, Jepang.
Kontak: muhamadukhtary(at)gmail(dot)com.



