Adakah di antara teman-teman yang pernah melihat ataupun mengenakan topi seperti pada gambar? Sepertinya semua telah mengenali bentuk dari topi pada gambar, bukan? Ya, topi tersebut cukup jelas berbentuk kerucut. Lalu, apa yang istimewa dari kerucut ini?

Ada yang menarik tentang bentuk kerucut ini. Apollonius (225 S.M), seorang Yunani kuno, menggambarkan bagaimana lingkaran, elips, parabola, dan hiperbola dapat dibentuk dengan memotong bidang datar sebuah kerucut dari beberapa arah sudut atau bisa disebut irisan kerucut (conic sections).
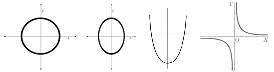
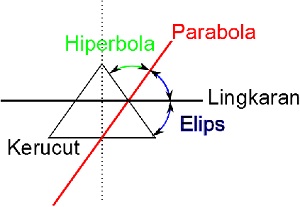
Mari kita ambil satu bidang pada kerucut yang melalui titik A. Jika titik A tegak lurus dengan sumbu kerucut, maka akan terbentuk sebuah lingkaran. Jika bidang potong yang melalui titik A tepat sejajar dengan salah satu elemen dari sisi kerucut, kita akan mendapatkan parabola. Jika kita memotong tegak lurus dengan titik A maka akan menghasilkan hiperbola. Sementara itu, bidang yang lain akan menghasilkan elips. Posisi-posisi bidang potong ini diilustrasikan pada gambar.
Nah, mari kita melakukan eksperimen sederhana dengan melipat kertas yang membentuk irisan kerucut. Bahan yang kita butuhkan untuk eksperimen ini hanyalah beberapa lembar kertas, penggaris, jangka (atau koin), dan pensil. Pertama, mari kita mencoba untuk membuat bentuk parabola. Pada selembar kertas, gambarlah sebuah titik dan garis seperti pada gambar. Lipatlah kertas sehingga titik berimpit dengan garis.
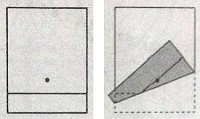
Jika kita lakukan berulang kali, lipatan-lipatan yang terbentuk akan membentuk garis-garis singgung parabola. Melalui eksperimen sederhana ini, kita dapat mengerti bahwa parabola ialah himpunan dari titik-titik yang titiknya berjarak sama dari sebuah titik tetap dan sebuah garis tetap.

Kedua, untuk membuat bentuk elips gambarlah lingkaran dan sebuah titik di dalam lingkaran. Lipat bermacam-macam titik pada lingkaran ke sebuah titik di dalam lingkaran, lakukan secara berulang dan kita akan mendapatkan garis singgung elips.
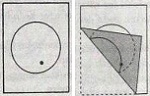
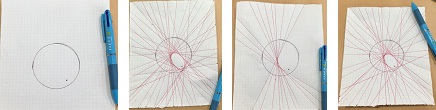
Dari eksperimen kedua ini, kita dapat simpulkan bahwa elips ialah himpunan titik-titik yang jumlah jarak-jarak dari setiap titiknya terhadap dua buah titik tetap adalah konstan. Dengan metode yang sama kita akan mendapatkan garis singgung untuk hiperbola. Namun, kini kita letakkan titik di luar lingkaran.
Silakan dipraktikkan sendiri, apa yang terjadi jika teman-teman melipat kertas pada gambar terakhir sehingga titik selalu berimpit dengan busur lingkaran. Melalui praktik ini kita dapat memahami bahwa hiperbola ialah himpunan titik-titik yang selisih jarak-jarak dari setiap titiknya terhadap dua buah titik tetap adalah konstan. Menarik ya, tanpa persaman kita bisa mendefinsikan bangun geometri! Bagaimana dengan geometri lingkaran? Silakan teman-teman coba dulu selesaikan sendiri, ya!
Penulis:
Evelyn Pratami Sinaga, Mahasiswa Fisika di Tohoku University, Jepang.
Kontak: evelynpratami(at)gmail.com


