Pernahkan teman-teman mendengar istilah “Deep Blue”? Deep Blue adalah kecerdasan buatan pertama dalam permainan catur yang dapat mengalahkan juara dunia catur Garry Kasparov. Deep Blue pertama kali mengalahkan Kasparov pada tanggal 10 Februari 1996, dalam ronde pertama dari 6 ronde pertandingan catur, walaupun pada akhirnya pertandingan 6 ronde ini dimenangkan oleh Garry Kasparov dengan skor 4-2.
Nah, bagaimana sih caranya Deep Blue bisa mengalahkan Kasparov dalam pertandingan catur tersebut? Tentunya Deep Blue menggunakan algoritma yang rumit untuk bisa mengalahkan juara dunia catur ini.
Dalam artikel ini kita akan belajar cara membuat kecerdasan buatan sederhana dengan menggunakan algoritma pencarian dasar bernama “Minimax”. Algoritma Minimax ini digunakan untuk membuat kecerdasan buatan dalam sebuah permainan, khususnya permainan yang dimainkan oleh 2 orang dan tidak ada unsur keberuntungan di dalam permainan tersebut seperti catur, othello, dan Igo.
Pohon permainan
Sebelum membahas algoritma pencarian Minimax kita akan membahas struktur data bernama “Pohon Permainan” yang digunakan dalam algoritma ini. Seperti namanya, pohon permainan terbentuk dari sebuah akar yang membentuk cabang-cabang dan terdapat daun di ujung-ujung cabangnya.
Cabang pada pohon permainan menunjukkan pilihan langkah yang dapat dilakukan pemain dalam permainan, dan titik percabangan menunjukkan kondisi dari permainan ketika pemain akan melakukan langkah. Akar dalam pohon permainan adalah titik percabangan pertama, dan menunjukkan kondisi awal dari permainan. Sebaliknya, daun adalah titik akhir dari sebuah cabang, dan tidak ada lagi percabangan setelah titik ini. Jadi, daun menunjukkan kondisi akhir dari permainan, yaitu kondisi ketika pemenang sudah ditentukan, atau permainan berakhir seri.
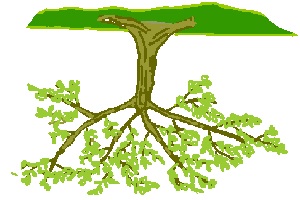
Berbeda dengan pohon biasa, akar dalam pohon permainan menempati posisi tertinggi, dan membentuk cabang ke arah bawah. Setiap titik percabangan membentuk cabang satu tingkat ke arah bawah yang terhubung dengan titik percabangan lain atau daun. Tingkatan titik percabangan di pohon permainan ini kita sebut sebagai kedalaman.
Kedalaman dari setiap titik percabangan dan daun menunjukkan jumlah langkah yang telah dilakukan pemain sampai mencapai titik atau daun tersebut. Jadi, akar memiliki kedalaman 0 dan akan terus bertambah setiap adanya percabangan. Untuk memudahkan penjelasan, titik percabangan atau daun yang terhubung langsung di bawah sebuah titik percabangan kita sebut sebagai anak.
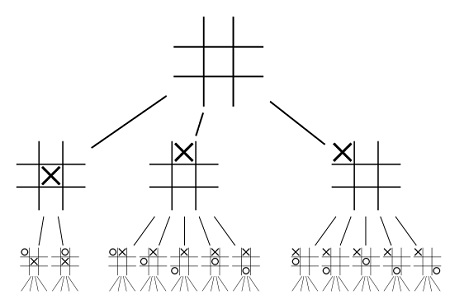
Sebagai contoh, mari kita membuat pohon permainan tic-tac-toe. Permainan tic-tac-toe dimulai dari kondisi ketika semua kotak kosong sebagai akar dari pohon permainan ini. Dari kondisi awal pemain pertama memiliki 3 pilihan langkah, yaitu mengisi kotak di pojok, di sisi, atau di tengah kotak permainan. Jadi, akar dari pohon permainan ini terhubung dengan 3 titik di bawahnya.
Untuk setiap titik yang berada 1 tingkat di bawah akar, pemain kedua memiliki jumlah pilihan langkah berbeda-beda, tergantung dari langkah yang dilakukan oleh pemain pertama. Jadi, masing-masing titik percabangan akan terhubung dengan sejumlah titik di bawahnya sesuai dengan jumlah pilihan langkah yang dapat dilakukan. Hal ini dilakukan berulang-ulang sampai semua kotak terisi atau salah satu pemain membuat garis lurus secara vertikal, horizontal, atau diagonal, yang merupakan daun dari pohon permainan tic-tac-toe.
Algoritma Minimax
Dengan menggunakan pohon permainan, bagaimana sih kita membuat kecerdasan buatan yang dapat mencari langkah terbaik untuk memenangkan permainan? Langkah terbaik dapat dicari dengan mengecek seluruh titik dan daun yang ada dalam pohon permainan. Tetapi untuk mengecek seluruh titik pada pohon permainan diperlukan waktu yang lama.
Nah, sebenarnya kita tidak perlu memeriksa semua seluruh titik pada pohon permainan untuk mencari langkah terbaik pada permainan tersebut. Salah satu caranya adalah dengan menggunakan algoritma Minimax, yang merupakan algoritma dasar dari algoritma-algoritma pencarian lainnya yang digunakan untuk membuat kecerdasan buatan yang lebih hebat.
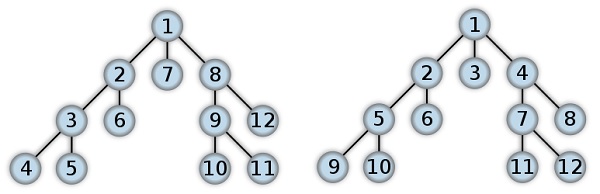
Ada dua macam metode untuk menentukan urutan pencarian dalam algoritma Minimax, yaitu Depth-first Search (DFS) dan Breadth-first Search (BFS). Sesuai namanya, DFS adalah urutan pencarian yang mendahulukan kedalaman. Ketika sebuah titik diperiksa, titik berikutnya yang akan diprioritaskan untuk diperiksa adalah titik di bawahnya, bukan titik di sebelahnya. Sebaliknya, dalam BFS titik yang diprioritaskan untuk diperiksa adalah titik dengan kedalaman yang sama. Setelah semua titik dengan kedalaman yang sama diperiksa, barulah titik yang dibawah diperiksa. Dalam tulisan ini kita akan menggunakan DFS sebagai urutan pencarian algoritma minimax.
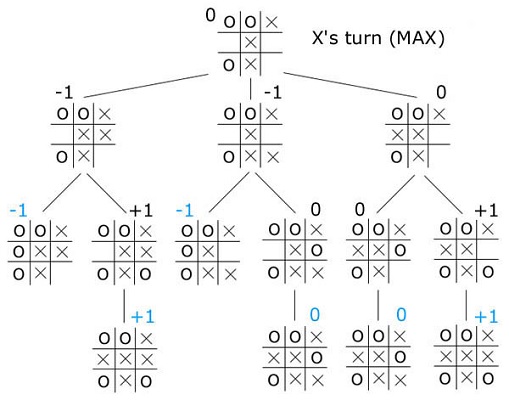
Algoritma Minimax dimulai dengan membagi titik-titik pada pohon permainan menjadi dua jenis, yaitu titik minimum dan titik maksimum. Titik minimum adalah titik tempat giliran pemain lawan melakukan langkah, sedangkan titik maksimum adalah titik tempat kecerdasan buatan melakukan langkah. Pencarian dimulai dengan memeriksa titik tempat kecerdasan buatan akan melalukan langkah. Pemeriksaan sebuah titik dilakukan dengan langkah berikut:
- Jika titik tersebut adalah titik akhir, kita tentukan nilai titik itu (1 menang, 0 seri, -1 kalah).
- Jika titik tersebut bukan titik akhir, kita periksa salah satu anak dari titik ini. Setelah kita memeriksa salah satu anak dari titik ini, kita perbarui nilai dari titik ini.
Cara memperbarui nilai dari sebuah titik tergantung dari jenis titik tersebut. Apabila titik ini adalah titik minimum, nilai dari titik ini adalah nilai terkecil dari seluruh nilai anak-anak yang sudah diperiksa. Sebaliknya, apabila titik ini adalah titik maksimum, nilai dari titik ini adalah nilai terbesar dari seluruh nilai anak-anak yang sudah diperiksa.
Pada titik minimum, apabila nilai dari salah satu anaknya adalah -1, kita tidak perlu memeriksa anak-anak lainnya dan menetapkan nilai titik tersebut -1, karena tidak ada nilai yang lebih kecil dari -1. Dengan alasan yang sama, kita tidak perlu memeriksa lagi anak-anak dari titik maksimum tersebut apabila nilai dari salah satu anak dari titik ini adalah 1. Dengan begitu, kita dapat melewati pemeriksaan titik-titik yang tidak perlu dan mempercepat pencarian secara keseluruhan.
Bahan bacaan:
- https://en.wikipedia.org/wiki/Game_tree
- https://en.wikipedia.org/wiki/Depth-first_search
- https://en.wikipedia.org/wiki/Breadth-first_search
- https://www.ocf.berkeley.edu/~yosenl/extras/alphabeta/alphabeta.html
Penulis:
Diptarama, Mahasiswa S3 Jurusan Sains Informasi, Tohoku University, Jepang.
Kontak: dream132(at)yahoo(dot)com.



