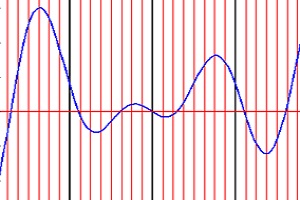
Dalam penelitian yang melibatkan analisis kuantitatif, tidak jarang seseorang dihadapkan pada masalah matematika yang sangat rumit. Contohnya adalah menyelesaikan persamaan yang melibatkan fungsi polinomial (x, x2, … , xn), fungsi trigonometri (sin x, cos x, tan x), fungsi eksponen dan logaritma, dan bahkan fungsi transenden [xx, (sin x)cos x, dll]. Bergelut dengan persoalan matematika seperti ini tidak jarang menyebabkan kita menjadi frustrasi.
Namun, dengan teknologi modern, kita dapat meminta bantuan komputer untuk menyelesaikan berbagai persoalan matematika yang tidak terpecahkan dengan hitungan tangan. Dalam artikel ini, kita akan belajar bagaimana cara mencari akar-akar suatu persamaan dengan metode grafik.
Nah, yang kita butuhkan adalah sebuah komputer dan sebuah perangkat lunak pendukung. Penulis menyarankan penggunaan perangkat lunak pembuat plot bernama “Grace”. Perangkat lunak ini dapat diunduh secara gratis (http://sourceforge.net/projects/qtgrace/) dan dapat dijalankan pada berbagai sistem, mulai dari Windows, Linux, hingga Mac.
Menggambar grafik dan mencari akar-akar persamaan
Jika teman-teman sudah mengunduh Grace, itu artinya teman-teman sudah siap untuk mengikuti tutorial ini. Silakan buka aplikasi bernama qtgrace.exe (untuk Windows) pada folder berikut ini:
<Download_folder>\qtgrace_windows_binary_024\bin.
Contoh tampilan awal ditunjukkan seperti pada Gambar 1.
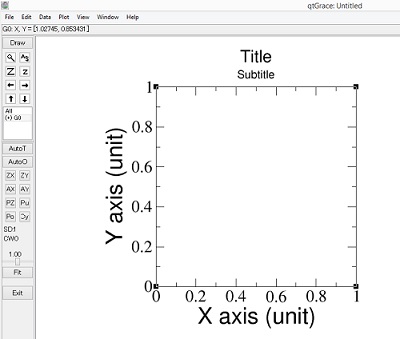
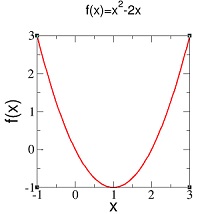
Kalau kita tidak melihat tampilan awal yang sama seperti pada gambar 1, yang tidak sama dengan yang kalian punya, kita dapat mengaturnya dengan mengganti file “Default.agr” melalui File -> Open -> Default.agr. Untuk menggambar sebuah fungsi, misalnya: f(x) = x2 – 2x, teman-teman dapat melakukan langkah-langkah berikut.
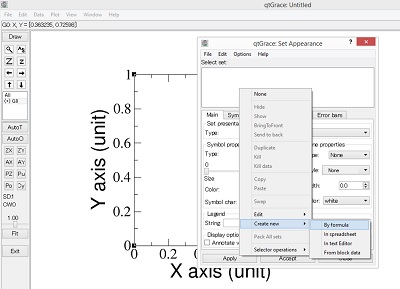
1) Tekan panel Plot -> Set appearance. Klik kanan pada Select set -> Create New -> By formula. Ilustrasinya seperti pada Gambar 2.
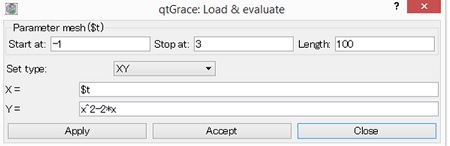
2) Isi parameter yang sesuai, kemudian tekan tombol Accept dan Close.
3) Teman-teman akan mendapatkan plot seperti pada Gambar 4.
Warna plot dan garis kurva dapat diubah sesuai selera pada menu Plot -> Set appearance -> Line properties.
Misalkan kita ingin mencari akar-akar persamaan f(x) = x2 – 2x = 0, kita dapat membuat garis bantu dengan mengaktifkan grid lines pada sumbu-x. Klik cursor di sumbu-x dua kali (double click), lalu pilih Tick marks -> Draw grid lines seperti ditunjukkan pada Gambar 5.
Dapat kita lihat bahwa nilai yang memenuhi f(x) = 0 adalah x = 0 dan x = 2.
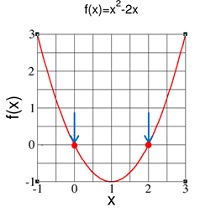
Hasil pada Gambar 6 cocok juga dengan perhitungan secara manual,
x2 – 2x = 0
x(x – 2) = 0
yang menghasilkan akar-akar x = 0 dan x = 2.
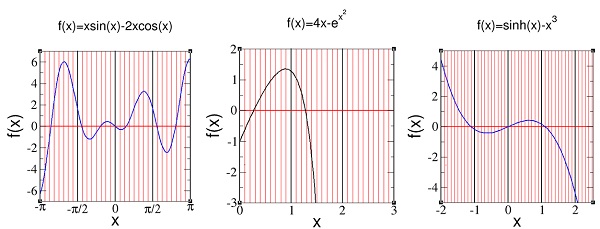
Nah, hal yang seru dari “permainan” ini, kita dapat mengulanginya untuk mencari akar-akar berbagai macam fungsi. Contoh-contohnya ditunjukkan pada gambar 7. Kini dengan metode grafik, fungsi sesulit apapun dapat dicari akar-akarnya.
Mencari solusi dari persamaan simultan
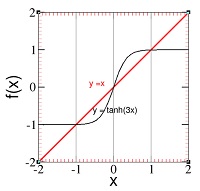
Sekarang kita coba pecahkan persoalan yang lebih rumit, yaitu mencari solusi persamaan simultan. Contoh persamaan simultan adalah
y = tanh(3x) …(1)
y = x …(2)
Kalau kita cari solusi persamaan simultan ini dengan hitungan tangan, tampaknya akan sulit. Namun, dengan metode grafik, untuk mencari nilai x yang memenuhi persamaan (1) dan (2) secara sekaligus, kita cukup menggambar dua garis (1) dan (2), dan mencari titik perpotongan kedua garis tersebut. Jika kita perhatikan Gambar 8, cukup jelas terlihat bahwa solusi persamaan simultan ini adalah x = -1, x = 0, dan x = 1.
Bagaimana teman? Seru, bukan? Ternyata kita bisa menyelesaikan persamaan-persamaan yang sulit dengan metode grafik. Teman-teman dapat mencoba sendiri di rumah untuk menyelesaikan persamaan-persamaan sulit lainnya.
Bahan bacaan:
Penulis:
Eddwi Hesky Hasdeo, Mahasiswa S3 Jurusan Fisika Tohoku University.
Kontak: heskyzone(at)gmail(dot)com