Pernah melihat matahari terbenam (sunset) dalam hidupmu sejauh ini? Pasti jawabannya sudah. Sangat indah, bukan? Apalagi ketika kita melihatnya di pantai. Bagaimana dengan melihat matahari terbit (sunrise)? Pasti sudah juga, dong. Akan tetapi, dalam satu hari saja, berapa kalikah kita bisa melihat matahari terbit dan terbenam? Satu kali? Dua kali? Mari kita bahas.
International Space Station (ISS), yang berada pada ketinggian kurang lebih sekitar 420 km di atas bumi, mengorbit bumi dengan kecepatan sangat tinggi, 8 km/s. Stasiun ini mengelilingi bumi dengan sedemikian cepatnya sehingga para astronot yang tinggal di sana dalam 24 jam bisa melihat matahari terbit dan terbenam tidak hanya sekali, tetapi 16 kali.
“Wah, nggak terima deh, ini kan karena mereka berada di luar angkasa, karena mereka mengitari bumi dengan cepat. Karena… karena…. Pokoknya ini nggak dihitung,” mungkin begitu gumam kita. Sabar, tidak perlu iri. Kita yang berada di permukaan bumi juga bisa dengan mudah melihat matahari terbit dan atau terbenam lebih dari satu kali dalam sehari. Bagaimana caranya? Rupanya dengan memanfaatkan bangunan tinggi, kita bisa melihat lebih dari satu kali sunrise dan sunset!
Matahari terbenam dua kali?
Mari kita lihat bangunan tertinggi yang pernah dibuat oleh manusia: Burj Khalifa di Dubai, Uni Emirat Arab. Bangunan dengan tinggi 830 meter ini sangat memukau. Kita bisa melihat matahari terbenam di lantai paling bawah, kemudian naik elevator super cepat ke lantai paling atas. Dari titik tertinggi itu arahkan pandangan ke horizon, dan kita akan melihat matahari yang sama terbenam untuk kedua kalinya.
Perbedaan waktu terbenamnya matahari di lantai paling bawah dan lantai paling atas sangat signifikan. Majelis Ulama Dubai, pada saat bulan Ramadhan, mengeluarkan peraturan yang cukup unik mengenai waktu buka puasa. Penghuni yang tinggal di lantai 80-150 harus menunda waktu buka puasa mereka selama 2 menit, sedangkan penghuni lantai 151-160 selama 3 menit. Ini disebabkan pada waktu yang sama, saat matahari telah terbenam di lantai bawah, matahari belum terbenam di lantai bagian atas. Unik, bukan?
Tentu saja kita tidak perlu pergi ke Dubai untuk melihat fenomena matahari terbenam dua kali ini. Mengapa? Karena ketinggian yang dibutuhkan untuk melihat matahari terbenam dua kali sebenarnya hanya sekitar tinggi tubuh kita.
Bagaimana caranya? Kita mulai dengan tidur tengkurap dan kepala menghadap horizon. Saksikan matahari terbenam dan jangan takut untuk memandang matahari langsung karena matahari sore aman untuk dipandang. Saat bagian terakhir dari matahari menghilang di horizon, segeralah berdiri dan lihatlah matahari kembali muncul atau ada bagiannya yang kembali muncul.
Menariknya, cara melihat matahari terbenam dua kali itu bisa diaplikasikan juga untuk matahari terbit. Prinsipnya sama saja. Setelah seluruh matahari muncul dari horizon, segera berdiri dan lihat matahari terbit lagi.
Bagaimana penjelasannya?
Perhatikan gambar di bawah. Pada gambar ditunjukkan tongkat berwarna pink. Dari posisi tongkat tersebut, pandangan ke arah matahari akan berubah karena Bumi berputar. Dengan perputaran bumi berlawanan jarum jam seperti pada gambar, matahari terbenam akan terlihat pada posisi 2. Jika pada posisi 2 panjang tongkat pink ditambah (garis kuning), matahari akan kembali muncul, dan akan terbenam untuk kedua kalinya (posisi 3).
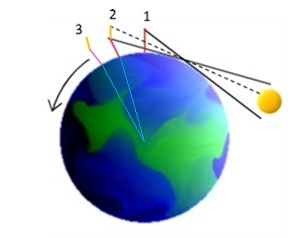
Hal yang lebih seru lagi, jika kita hitung tinggi kita, dan waktu antara posisi 2-3, kita bisa mengukur jari jari bumi lho. Jadi, ketika kita pergi ke pantai, kita tidak hanya bisa melihat matahari terbit atau tenggelam dua kali, tetapi juga kita bisa mengukur jari-jari bumi. Jangan lupa untuk bawa meteran dan stopwatch!
Let’s do it!
Cara mengukur jari-jari bumi
Alat yang diperlukan untuk kegiatan ini adalah stopwatch, meteran, dan teman yang “baik”. Langkah-langkahnya sebagai berikut:
- Pergilah ke pantai bersama teman, dan jangan lupa membawa alat yang diperlukan. Penting untuk diperhatikan bahwa pantai yang dimaksud adalah pantai yang mataharinya terbenam di laut, bukan gunung/pulau.
- Posisikan diri tengkurap menghadap matahari yang terbenam. Suruh teman untuk mengukur ketinggian mata dari tanah.
- Saksikan matahari terbenam, siapkan stopwatch.
- Saat matahari sudah benar-benar terbenam, nyalakan stopwatch dan segera berdiri sedemikian rupa sehingga posisi mata sekarang berada di atas posisi mata saat tengkurap.
- Saksikan matahari terbenam lagi. Saat benar benar terbenam, hentikan stopwatch.
- Suruh teman ukur ketinggian mata saat berdiri.
- Catat semua data, misalkan waktu = $latex t$, tinggi mata saat tengkurap = $latex h_1$ dan tinggi mata saat berdiri = $latex h_2$.
Oh satu hal lagi terlewat. Sebelum kita mulai menghitung jari-jari bumi, tentunya kita harus mengetahui cara mengukur jarak dari kita berdiri ke horizon. Perhatikan gambar di bawah.
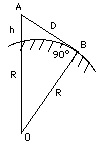
$latex D={\rm jarak\ ke\ horizon,}\ R ={\rm jari-jari\ bumi,}\ h ={\rm tinggi\ mata} \newline$
Dengan rumus Pythagoras, kita bisa peroleh:
$latex {\left ( {\rm OA} \right) }^{2} = {\left ( {\rm AB} \right) }^{2} + {\left ( {\rm OB} \right) }^{2} \newline$
$latex {\left ( D + h \right ) }^{2} = {D}^{2}+ {R}^{2} \newline$
$latex {D}^{2} + 2Rh + {h}^{2} = {D}^{2}+ {R}^{2} \newline$
$latex h \left ( 2R + h \right ) = {D}^{2} \newline$
Karena nilai $latex R$ jauh lebih besar dari $latex h$, kita bisa mengganti $latex 2R+ h$ menjadi cukup $latex 2R$ saja. Dengan demikian,
$latex 2Rh = {D}^{2} \newline$
$latex D = \sqrt{2Rh}$
Kembali ke ilustrasi mula-mula, dengan menghitung jarak ke horizon di posisi 2 dan 3 kita bisa tahu jarak yang ditempuh Bumi dalam selang waktu yang terukur di stopwatch.
 Kita bisa gunakan perbandingan sudut yang sederhana:
Kita bisa gunakan perbandingan sudut yang sederhana:
$latex \displaystyle \frac{{D}_{3}-{D}_{2}}{t} = \frac{\rm keliling\ bumi}{24 {\rm jam}}$
$latex \displaystyle \frac{\sqrt{2 R h_1} – \sqrt{2 R h_2}}{t} = \frac{2\pi R}{3600 \times 24}$
$latex \displaystyle \frac{\sqrt{R} \times \left ( \sqrt{2h_{1}} – \sqrt{2h_{2}}\right )}{R} = \frac{2\pi t}{3600 \times 24}$
$latex \displaystyle R = {\left ( \frac { \left ( \sqrt{2h_{1}} – \sqrt{2h_{2}}\right ) \times 3600 \times 24}{2 \pi t}\right )}^{2}$
Akhirnya, kita mendapatkan sebuah rumus untuk mencari jari-jari bumi. Tinggal masukkan saja data hasil pengamatan tadi, dan kita berhasil melihat matahari terbenam dua kali sekaligus mengukur jari-jari bumi.
Bahan bacaan:
- http://www.astro.princeton.edu/~dns/teachersguide/MeasECAct.html
- http://www-spof.gsfc.nasa.gov/stargaze/Shorizon.html
- http://www.darylscience.com/downloads/DblSunset.pdf
Penulis:
Rahmanto, pelajar di JASSO Tokyo Japanese Language Education Center, Tokyo, Jepang.
Kontak: rahmanto(at)outlook.com



