Jika teman-teman berjalan melintasi halaman perkantoran, pasti pernah melihat pagar berbentuk rantai seperti gambar di bawah.

Jalinan rantai tersebut membentuk sebuah kurva yang disebut dengan katenari (bahasa Inggris: catenary). Pada tulisan kali ini, kita akan bersama-sama menemukan persamaan kurva sebuah katenari. Mari siapkan pensil dan kertas supaya bisa memahami penurunan persamaannya.
Dalam bidang fisika dan geometri, katenari adalah kurva yang terbentuk oleh kabel/rantai/tali yang terikat di kedua ujungnya dan dibebani oleh beratnya sendiri. Kabel ini dianggap memiliki kerapatan yang homogen. Kata “Katenari” sendiri berasal dari bahasa Latin catena yang berarti rantai. Kurva ini berbentuk U dan sangat mirip dengan parabola. Meski demikian, perumusan katenari dalam matematika sangat berbeda dengan persamaan parabola.
Sifat matematis dari katenari pertama kali dipelajari oleh Robert Hooke sekitar tahun 1670, tetapi persamaan untuk kurva katenari baru ditemukan pada tahun 1691 oleh Leibniz, Huygens dan Johann Bernoulli. Sering disebutkan bahwa ilmuwan hebat seperti Galileo pun pernah salah mengira bahwa rantai yang menggantung adalah parabola (dengan persamaan dasar $latex y = ax^2 + bx + c$). Hingga akhirnya pada tahun 1669, Joachim Jungius membuktikan bahwa rantai yang menggantung bukanlah parabola, melainkan kurva katenari.
Sekarang kita akan membahas kurva katenari dari sudut pandang matematika. Kita akan belajar untuk mencari rumus kurva katenari. Pertama-tama mari kita membagi bagian katenari yang simetris ke dalam dua bagian dan memberi titik C sebagai titik terbawah dari katenari tersebut seperti pada gambar.
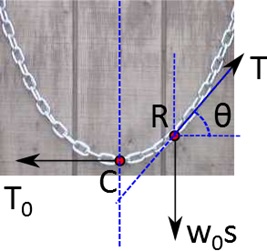
Berdasarkan diagram, gaya tarik $latex T_0$ bekerja secara horizontal ke kiri di titik C. Kini kita meninjau sembarang titik R sambil memperhatikan gaya-gaya yang bekerja di titik tersebut. Pertama, ada gaya $latex T$ yang bekerja ke kanan atas dengan sudut $latex \theta$ terhadap horizontal. Kedua, ada gaya berat rantai $latex w_0 s$. Dalam hal ini kita asumsikan katenari memiliki kerapatan yang homogen, $latex w_0$, dengan dimensi massa per satuan panjang. Panjang panjang jalinan rantai di sini adalah $latex s$.
Karena rantai diasumsikan tidak bergerak, penjumlahan dari gaya horizontal dan vertikal pastilah nol, sehingga didapatkan persamaan
[1]… $latex T \cos(\theta) = T_0$ dan $latex T \sin(\theta) = w_0 s$.
Kita akan menghilangkan variabel $latex T$ dengan pembagian. Dengan demikian, persamaan (1) menjadi
[2]… $latex \tan(\theta) = \displaystyle \frac{w_0 s}{T_0}$.
Kita tulis ulang persamaan (2) menjadi bentuk turunan terhadap $latex x$ sehingga didapatkan persamaan sebagai berikut
[3]… $latex \displaystyle\frac{dy}{dx} = as$, dengan $latex a = \displaystyle\frac{w_0}{T_0}$.
Persamaan (3) juga kita turunkan terhadap $latex x$ sehingga menjadi
[4]… $latex \displaystyle \frac{d^2 y}{dx^2} = a \frac{ds}{dx} = a \sqrt{1 + \left(\frac{dy}{dx}\right)^2}$,
dan di sini $latex ds/dx = \sqrt{1+(dy/dx)^2}$ sesuai teorema Pythagoras.
Misalkan $latex p = dy/dx$, persamaan (4) berubah menjadi
[5]… $latex \displaystyle\frac{dp}{dx} = a \sqrt{1 + p^2}$.
Persamaan (5) dapat dicari solusinya dengan menggunakan metode pemisahan variabel, yaitu
$latex \displaystyle \int \frac{dp}{\sqrt{1+p^2}} = \int a dx$
Hasil integrasi di kedua ruas akan menjadi
[6]… $latex \sinh^{-1} (p) = a x + C_1$,
dengan $latex \sinh(x) = (e^x – e^{-x})/2$. Kemudian, dengan memilih titik $latex x = 0$, $latex p = 0$, maka $latex C_1 = 0$. Kita peroleh
[7]… $latex p = \sinh (a x)$.
Pada persamaan (5) kita memiliki $latex p = dy / dx$, maka persamaan (7) dapat berubah menjadi
[8]… $latex \displaystyle \frac{dy}{dx} = \sinh (ax)$
Kita dapat menemukan $latex y$ dengan mengintegralkan persamaan (8). Solusinya adalah
$latex \displaystyle y = \frac{1}{a} \cosh (a x) + {\rm konstanta}$,
dengan $latex \cosh (x) = (e^x + e^{-x})/2$. Persamaan yang terakhir ini merupakan persamaan kurva katenari yang telah ditemukan oleh para ilmuwan. Jelas sekali perbedaannya dengan persamaan parabola $latex y = ax^2 + bx + c$.
Setelah kita melihat katenari dari segi sejarah singkat dan matematika, mari kita lihat katenari di lingkungan sekitar kita. Tentu saja teman-teman pasti sudah dapat menebak bahwa katenari itu ada pada kabel, tali dan rantai yang menggantung, karena contoh-contoh ini telah disebutkan sebelumnya. Bagaimana dengan contoh yang lain? Apakah masih ada? Ternyata banyak. Mirip dengan contoh sebelumnya, katenari juga terdapat pada jaring laba-laba dan jembatan.

Selain itu, katenari menjadi inspirasi untuk seni bangunan. Yang paling sering menjadi inspirasi pada seni bangunan adalah katenari terbalik, sebagai sebuah atap, gerbang ataupun hanya berupa hiasan. Ketika dilihat dengan mata telanjang, bangunan ini memang terlihat seperti katenari terbalik. Namun, bangunan tersebut bukanlah katenari secara matematika karena bangunan ini memiliki kerapatan yang berbeda-beda. Sebenarnya bangunan-bangunan ini hanya mencoba meniru bentuk katenari yang indah dan unik.

Melalui contoh katenari ini kita bisa lihat bahwa matematika ternyata begitu dekat dengan lingkungan kita sehari-hari. Mari kita terus eksplorasi matematika tanpa kenal lelah! Semangat!
Bahan bacaan:
- http://mathfaculty.fullerton.edu/mathews/n2003/CatenaryMod.html
- http://en.wikipedia.org/wiki/Catenary
- G. F. Simmons, Calculus Gems: Brief Lives and Memorable Mathematics, New York: McGraw Hill (1992).
Penulis:
Reyna Marsya Quita, mahasiswa master di Jurusan Matematika, Universitas Brawijaya, Malang.
Kontak: reynaquita2905(at)gmail.com



