Matematika dan Seni

Matematika dan seni merupakan dua bidang yang sepintas tidak berhubungan. Benarkah seperti itu? Mari kita perhatikan beberapa objek seni. Tak disangka ternyata objek-objek ini mengandung aspek matematis, lho!

1. Piramida

Salah satu hubungan antara seni dan matematika hadir dalam Piramida. Heroditus, yang disebut bapak sejarah, adalah orang pertama yang menulis tentang piramida sekitar 440 SM. Piramida dipercaya memiliki banyak cerita. Contohnya adalah bahwa piramida merupakan model bumi, bahwa poros mereka selaras dengan bintang tertentu, bahwa mereka adalah bagian dari sistem navigasi untuk membantu wisatawan di padang pasir menemukan jalan, dan masih banyak lagi.

Pada bagian ini kita akan membuktikan ternyata piramida mengandung golden ratio. Golden ratio adalah bilangan irasional yang nilainya mendekati 1,618. Seputar golden ratio ini pernah dibahas di rubrik matematika majalah 1000guru edisi bulan Juli 2013.

Untuk menunjukkan golden ratio pada piramida, kita memerlukan contoh. Salah satu contohnya adalah Piramida Agung Cheops. Berdasarkan penelitian, piramida ini memiliki tinggi = 146,52 m, dan lebar alas = 230,36 m.

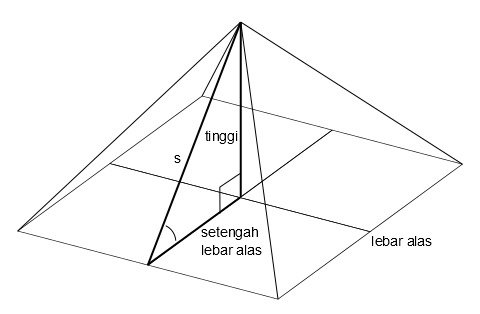
Dengan mudah, kita dapat menghitung setengah lebar alas, yaitu 230,36 m / 2 = 115,18 m. Berdasarkan rumus Phytagoras, nilai s juga dapat kita ketahui, yaitu

$latex s^2 = 146,52^2 + 115.18^2 = 34.73~{\rm m}^2$

$latex \therefore s = 186,37~{\rm m}$

Kemudian, dengan membagi kemiringan s dengan setengah lebar alas, didapatkan

$latex \displaystyle \frac{186,37~{\rm m}}{115,18~{\rm m}} = 1,618$

Nilai ini tidak lain merupakan nilai dari golden ratio. Hal ini membuktikan bahwa Piramida memiliki koneksi dengan matematika.

2. Lukisan Mona Lisa

Tentu kita sudah tahu siapa pelukis Monalisa, Leonardo Da Vinci. Leonardo (1452-1519) adalah seorang Italia. Ia sangat terampil dalam berbagai bidang: matematika, filsafat, arsitektur sipil dan militer, melukis, memahat, ilmu pengetahuan, menciptakan musik, dan mendesain senjata. Leonardo sendiri paling terkenal sebagai pelukis. Uniknya, ia sering memasukkan konsep-konsep matematika dalam karya seninya meskipun tidak pernah menerima pelatihan matematika secara formal. Pada lukisan Monalisa, ketidaksesuaian antara latar belakang kiri dan kanan menciptakan ilusi perspektif dan kedalaman.

Banyak yang meyakini bahwa Leonardo secara sengaja menciptakan lukisan ini sesuai dengan golden rectangle sebagai penyatuan matematika dan seni. Golden rectangle adalah sebuah segiempat yang salah satu panjang sisinya memiliki nilai golden ratio (1,618). Untuk lebih jelas perhatikan gambar berikut.

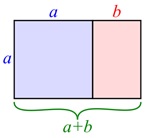
Jika nilai dan , segiempat biru dan merah menjadi golden rectangle karena salah satu sisinya (yaitu ) memiliki nilai golden ratio. Segiempat merah juga merupakan golden rectangle dengan alasan yang sama.

Sekarang kita kembali kepada lukisan Monalisa. Sebuah golden rectangle dapat dibentuk pada lukisan ini. Untuk membentuk segiempat dapat diambil garis dari pergelangan tangan kanan, menuju ke siku kiri, kemudian garis ditarik ke atas sampai puncak kepala.

Mona Lisa dan golden rectangle — Mona Lisa dan *golden rectangle*.

Kita bisa lihat setiap garis dari segiempat tersebut memotong titik-titik yang penting pada lukisan Mona Lisa, yaitu dagu, mata, hidung dan senyum pada bibirnya. Sekali lagi, hal ini menunjukkan seni dan matematika memang berkaitan.

3. Seni Fraktal

Setelah membahas dua objek yang telah eksis bertahun-tahun yang lalu, mari kita kembali ke tahun milenium. Kevin Gross, yang berasal dari Dakota selatan, tidak menggunakan kuas ataupun kanvas untuk membuat lukisan, melainkan matematika. Bagaimana bisa? Ternyata, Kevin menggunakan seni fraktal. Seni fraktal adalah bentuk seni algoritma yang dibentuk dengan menghitung objek fraktal dan hasil akhirnya adalah gambar, animasi, ataupun media. Tujuan Kevin melukis menggunakan seni fraktal adalah ia ingin menunjukkan bahwa matematika adalah seni. Contoh yang paling terkenal dari seni fraktal adalah Mandelbrot set, dinamai sesuai dengan matematikawan Benoit Mandelbrot, yang mempelajari dan mempopulerkan himpunan ini. Mandelbrot set merupakan himpunan yang diperoleh dari persamaan kuadrat rekursif:

$latex z_{n+1} = z_n^2 + C$

dengan $latex z_0 = C$. Parameter $latex C$ ada di bidang kompleks dan orbit $latex z_n$ terbatas.

Penjelasan lebih rinci mengenai fraktal pun pernah dibahas pada rubrik matematika majalah 1000guru edisi bulan Januari 2012.

Masih banyak lagi contoh-contoh relasi antara matematika dan seni, misalnya perspektif dan pola. Silakan teman-teman selidiki sendiri ya!

Bahan bacaan:

Penulis:
Reyna Marsya Quita, mahasiswa master di Jurusan Matematika, Universitas Brawijaya, Malang.
Kontak: reynaquita2905(at)gmail.com

Matematika dan Seni