God does not play dice
[Albert Einstein]
Mari kita lakukan permainan sebagai berikut. Lihat gambar di bawah. Kita mempunyai papan piringan yang dibagi menjadi 4 bagian dan kita beri label A, B, C, dan D. Kemudian, piringan itu kita taruh di tembok sedemikian rupa sehingga kita bisa putar. Yang kita lakukan adalah, ketika piringan itu berputar, melemparkan panah dan mencatat belahan lokasi panah kita mendarat. Jadi, semacam permainan dart. Umpamakan dalam satu permainan, kita mempunyai 10 anak panah.
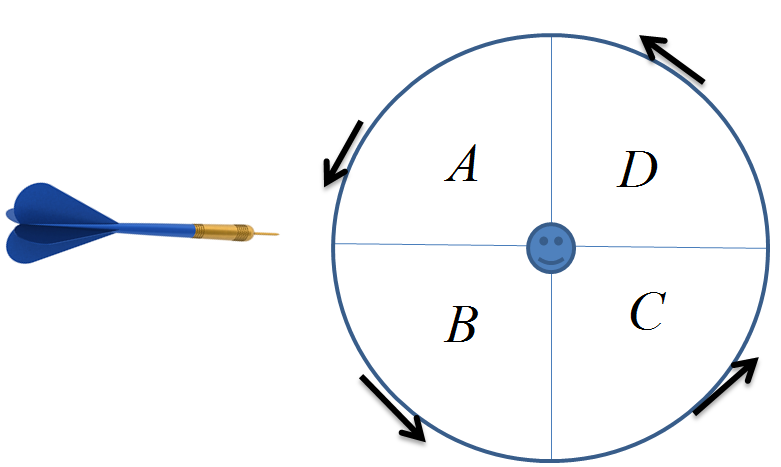
Pertanyaan yang bisa kita ajukan adalah bagaimana anak-anak panah itu terdistribusikan di papan piringan? Berapa anak panah yang mendarat di bagaian A, B, C, dan D setelah 10 anak panah itu kita lempar semua. Tentu saja, kalau laju putaran piringan sangat lambat, kita bisa mengincar belahan tertentu sehingga mendapatkan distribusi anak panah sesuai dengan apa yang kita inginkan. Bagaimana kalau piringan kita putar cukup cepat sehingga setiap anak panah yang kita lemparkan mendarat acak (random) di piringan? Bagaimanakah distribusi anak-anak panah di piringan setelah 10 anak panah kita lempar semua?
Pertanyaan di atas tentu saja tidak lengkap. Mengapa? Misalkan kita selesai melemparkan 10 anak panah dan kita catat distribusi dari lokasi mendarat di piringan. Kita dapatkan, misalnya bagian A kena 3 panah, bagian B kena 6 panah, bagian C kena 1 panah, dan bagian D tidak kena sama sekali. Kemudian, kita ambil semua anak-anak panah itu dan kita ulang percobaan dengan melempar anak-anak panah itu sampai habis. Apakah kita akan mendapatkan lagi distribusi yang sama dengan percobaan pertama? Tentu saja tidak. Begitu juga apabila kita ulang lagi percobaan tersebut. Di setiap percobaan kita akan mendapatkan distribusi anak-anak panah yang berbeda-beda. Artinya, jawaban dari pertanyaan di atas tidak unik. Oleh karena itu, pertanyaan yang kita ajukan di akhir paragraf sebelumnya bisa kita pertajam sebagai berikut: dari kemungkinan-kemungkinan distribusi 10 anak panah di papan piringan dengan 4 belahan, distribusi manakah yang paling mungkin? Inilah kurang lebih arti dari judul artikel ini.
Permainan dart kita di atas akan menjadi semakin menarik bila kita kasih skor/nilai untuk setiap belahan di papan piringan. Misalnya: kalau panah kita mengenai belahan A, kita mendapat skor 1, B skornya 2, C skornya 3, dan D skornya 4. Kemudian, kita buat syarat, misalnya lemparan yang sah adalah lemparan yang total skornya 30. Lemparan yang tidak memenuhi syarat di atas kita anggap tidak valid. Kemudian, kita kembali mengajukan pertanyaan: dari kemungkinan distribusi-distribusi 10 anak panah yang memenuhi syarat di atas, distribusi manakah yang paling mungkin?
Di artikel ini kita tidak akan membahas bagaimana pertanyaan sederhana di atas bisa diformulasikan dalam matematika dan dihitung solusinya. Yang menarik adalah banyak pertanyaan-pertanyaan menarik di sains yang bisa disederhanakan menjadi percobaan semacam di atas dan menghasilkan penemuan-penemuan yang sangat penting. Misalnya, bagaimana partikel-partikel di alam semesta terdistribusikan di berbagai nilai energi dengan peluang tertentu. Dengan kata lain: misalnya dalam suatu sistem ada N partikel dengan rata-rata energy E (sehingga total energy E kali N), berapa banyak partikel yang berpeluang memiliki energi X, Y, Z, dan seterusnya.
Ternyata, kalau kita asumsikan distribusi partikel-partikel itu ekuilibrium, pertanyaan di atas bisa kita jawab dengan mengajukan pertanyaan seperti dalam permainan kita: bagaimana distribusi dari partikel-partikel itu yang paling mungkin. Dalam konteks permainan kita, partikel-partikel ini adalah anak panah, alam semesta adalah si pemanah dan berbagai nilai dari energi yang bisa dimiliki partikel-partikel itu adalah skor-skor dari belahan-belahan piringan.
Ingat bahwa salah satu asumsi penting dari permainan kita adalah piringan kita putar dengan cepat sehingga setiap anak panah yang kita lempar mendarat dengan acak di piringan. Tentu saja kita bisa membuat permainan lain dengan semangat yang sama, misalnya melempar kelereng ke ember secara acak. Karena model permainan seperti ini bisa menjelaskan berbagai fenomena di alam semesta, seperti yang kita klaim di paragraf sebelumnya, seorang murid yang kritis mungkin akan bertanya, “Lho, kalau alam semesta seperti itu, apakah Tuhan bermain-main dengan dadu untuk mengatur alam semesta? Hanya Tuhan yang tahu.
Penulis:
Agung Budiyono, peneliti fisika independen dengan spesialisasi fondasi fisika kuantum dan mekanika statistik, saat ini bertempat tinggal di Juwana dan Sleman. Kontak: agungbymlati@gmail.com.



