Ada sebuah soal matematika yang sangat sederhana, begitu pula dengan solusinya. Akan tetapi, mungkin banyak di antara kita menjawabnya dengan sangat rumit.
Misalkan ada sebuah turnamen sepakbola antarkelas yang dilakukan dengan sistem gugur (sekali kalah langsung tersingkir). Turnamen itu diikuti oleh 25 kelas dalam satu sekolah. Berapa jumlah total pertandingan dalam turnamen tersebut hingga diperoleh satu juara? (tanpa perebutan tempat ketiga dan keempat)
Biasanya, banyak di antara kita memulai pemecahan masalah dengan cara mensimulasikan turnamen tersebut, salah satunya memasang-masangkan setiap tim untuk bertarung. Dalam kasus ini, ada 1 tim yang mendapat bye (tidak perlu bertanding, langsung lolos ke babak selanjutnya), dan ada 24 tim yang harus bertarung, sehingga jumlah pertandingan babak pertama adalah 12 pertandingan. Kemudian di babak kedua ada 13 tim tersisa yang komposisinya adalah 12 tim harus saling tarung (setara dengan 6 pertandingan), dan 1 tim mendapatkan bye. Sampai sini jumlah pertandingannya sudah 18 (= 12 + 6).
Di babak ketiga ada 7 tim tersisa dengan komposisi 6 tim harus saling tarung (setara dengan 3 pertandingan), dan 1 tim mendapatkan bye, sehingga jumlah pertandingan menjadi 21 (= 18 + 3). Sampai sini sudah tersisa 4 tim saja (semifinal), yang kita tahu hanya ada 2 pertandingan, sehingga jumlah pertandingan hingga babak semifinal adalah 23. Terakhir, 1 pertandingan babak final menggenapkan jumlah pertandingan menjadi totalnya 24. Merasa capek menghitung? Coba perhatikan diagramnya…
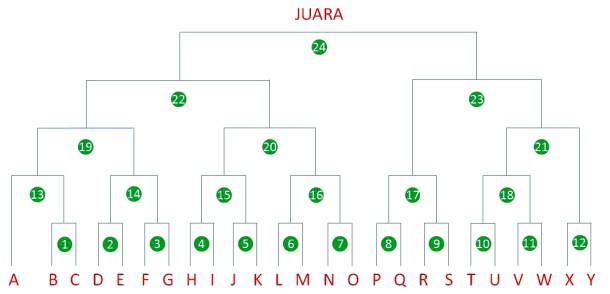
Bagaimana kalau ada lebih banyak tim yang bertanding? Katakanlah 141 tim bertarung dengan sistem gugur, berapa jumlah total pertandingannya?
Ternyata ada solusi yang lebih mudah…
Seringkali kita terjebak pada cara berpikir yang terlalu “alami”, tidak berani melakukan terobosan. Cobalah sekarang fokus pada jumlah “pecundang” (peserta yang kalah). Kita balik bertanya:
“Berapa jumlah pecundang dalam sebuah turnamen sistem gugur dengan 25 peserta sehingga ditemukan 1 juara?”
Jawabannya sederhana: ada 24 tim pecundang, dan ternyata sebanyak itu pula jumlah total pertandingan yang harus dilakukan dalam turnamen tersebut. Dengan demikian, kita sekarang tidak perlu repot berpikir lama-lama lagi ketika ditanya berapa jumlah total pertandingan jika ada 141 peserta. Jawabnya adalah 140 pertandingan, karena akan ada 140 pecundang (alias 140 kekalahan) dalam turnamen tersebut.
Buat orang-orang yang menjawab soal ini dengan cara yang pertama (diagramatik) mungkin akan bertanya pada dirinya sendiri:
“Mengapa saya tidak memikirkan cara pandang yang berbeda itu sejak awal?”
Catatan:
Tulisan ini diterbitkan ulang oleh penulis dengan beberapa perubahan dari salah satu arsip artikelnya di komunitas 102FM ITB.
Bahan bacaan:
- Alfred S. Posamentier, Math Wonders to Inspire Teachers and Students, ASCD, Vancouver (2003).
- http://www.mathsisfun.com
Penulis:
Ahmad Ridwan T. Nugraha, peneliti fisika, alumnus ITB dan Tohoku University.
Kontak: art.nugraha(at)gmail(dot)com.



