Pernahkah teman-teman bertemu dengan sebuah soal matematika yang tidak menyebutkan angka dan tidak memiliki pilihan jawaban berupa angka, melainkan meminta untuk diselesaikan secara aljabar dan hasil yang diinginkan adalah berupa persamaan dengan satu atau beberapa variabel? Mari kita bahas salah satu contohnya dalam artikel ini.
Pertanyaan:
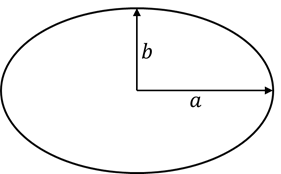
Sebuah elips memiliki sumbu semimayor a dan semiminor b. Manakah di antara pilihan berikut ini yang merupakan luas areanya (A)?
(i) A = ab2
(ii) A = a2 + b2
(iii) A= a3/b
(iv) A = 2ab
(v) A = πab
Teman-teman mungkin pada awalnya akan kebingungan memulai dari mana untuk membangun sebuah persamaan yang tepat dan sesuai dengan salah satu dari pilihan jawaban di atas. Akan tetapi, ada cara pemecahan yang lebih cepat dan praktis, yaitu dengan melakukan analisis dimensi pada pilihan-pilihan jawabannya satu per satu. Apa itu analisis dimensi? Lebih spesifik lagi, apa itu dimensi?
Konsep dimensi (dimensi fisis) diperkenalkan oleh Joseph Fourier pada 1822. Saat belajar tentang bangun-bangun geometris seperti persegi, segiempat, dan lingkaran kita sudah memahami istilah-istilah semacam sisi, panjang, lebar, diameter, dan keliling. Satuan dari mereka biasanya diberikan dalam meter, kilometer, inci, dll. Walaupun istilah-istilah tersebut dan satuannya bervariasi, jika kita perhatikan, semua istilah tersebut menyatakan panjang. Satuan yang diberikan pun adalah satuan-satuan panjang. Oleh karena itu, kita menyebut istilah-istilah di atas memiliki dimensi panjang (umumnya disimbolkan dengan L).
Contoh dimensi lainnya adalah waktu [T] yang sering muncul di dalam soal-soal matematika sebagai durasi waktu atau waktu tempuh dan memiliki satuan detik, jam, tahun, dll. Ada juga massa [M] yang seringkali dinyatakan dalam satuan gram, kilogram, ton, pon, dll.
Nah, pada dimensi panjang [L], kita bisa menyatakan luas sebagai [panjang]2 atau L2, dan volume sebagai [panjang]3 atau L3. Hal ini bisa dipahami dengan mudah jika kita memperhatikan satuan-satuan luas selalu dinyatakan dalam kuadrat dari satuan panjang (m2, km2, dll) dan volume selalu dinyatakan dalam kubik dari satuan panjang (m3, km3, dll)
Pemahaman di atas kemudian diterapkan dalam analisis dimensi. Kita diharuskan untuk mencari tahu dimensi sebenarnya dari suatu besaran untuk menyelesaikan suatu masalah. Besaran-besaran yang berdimensi sama dapat dibandingkan secara langsung (commensurable) dan satuan-satuannya dapat saling dikonversikan (sebagai contoh, 1 km = 1.000 m). Besaran-besaran berdimensi tak sama tidak dapat dibandingkan (incommensurable), seperti membandingkan mana yang lebih besar antara 1 meter tali dan 1 kilogram emas adalah kemustahilan.
Berikut ini kita akan mempraktikkan analisis dimensi untuk memecahkan permasalahan luas elips di atas. Tahapan penyelesaiannya tidak memerlukan perhitungan yang rumit, hanya mempertimbangkan kasus-kasus ekstrem yang sederhana, seperti jika salah satu atau beberapa variabelnya sama dengan 0.
Tahapan untuk memecahkan permasalahan di atas dengan mudah adalah sebagai berikut:
1. Uji Dimensi
Solusi yang diharapkan adalah luas, karena itu jawaban yang dibutuhkan harus memiliki dimensi L2. Pada sebuah elips, sumbu semi mayor a dan semi minor b menyatakan dimensi panjang L. Dari semua pilihan jawaban, (i) pastilah salah karena dimensinya bukan L2:
(i) ab2 = [L][L]2 = [L]3 (pasti salah)
(ii) a2 + b2 = [L]2 + [L]2 = 2[L]2 (mungkin benar)
(iii) a3/b = [L]3/[L] = [L]2 (mungkin benar)
(iv) 2ab = 2[L][L] = 2[L]2 (mungkin benar)
(v) πab = π[L][L] = π[L]2 (mungkin benar)
2. Uji Kondisi Ekstrem
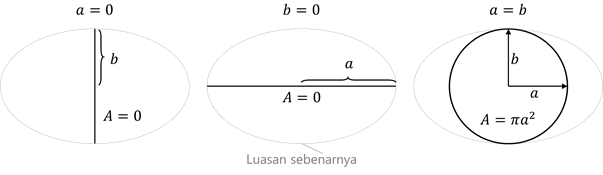
Berikutnya, kita akan menguji setiap pilihan jawaban dengan menerapkan kondisi-kondisi ekstrem yang mudah dipahami, yaitu a = 0, b = 0, dan a = b. Pada kondisi a = 0 dan b = 0, elips tersebut akan menjadi sangat tipis (infinitesimally thin ellipse) dan luasnya adalah nol. Jika a = b, elips tersebut akan menjadi sebuah lingkaran dengan luas A = πa2.
Untuk setiap pilihan jawaban yang tersisa, kita bisa analisis satu per satu.
(ii) Pada kondisi a = 0, solusi dari A = a2 + b2 adalah luas sebesar b2, bukan 0. Maka, pilihan (ii) ini salah.
(iii) A = a3/b menghasilkan luas nol pada kondisi a = 0. Hal yang sama seharusnya berlaku jika b = 0. Namun, ketika b = 0, kita dapati a3/b bernilai tak hingga, sehingga pilihan (iii) bukanlah solusi yang tepat.
(iv) Solusi A = 2ab memberikan luas area yang benar, A = 0, pada kondisi a = 0 dan b = 0. Namun, jika a = b, luas area yang dihasilkan adalah A = 2a2, bukan A = πa2 sebagaimana rumus luas lingkaran seharusnya. Jadi, (iv) juga bukan jawaban yang tepat.
(v) Semua kondisi a = 0, b = 0, dan a = b berlaku pada solusi A = πab Dengan demikian, inilah kandidat jawaban yang paling memungkinkan untuk permasalahan di atas. Dan sebenarnya secara matematis, solusi ini adalah luas area yang tepat untuk sebuah elips.
Contoh di atas adalah salah satu kasus mudah mengenai pemecahan soal menggunakan analisis dimensi dan kondisi-kondisi ekstrem. Soal-soal lainnya mungkin melibatkan lebih satu dimensi, seperti kecepatan [L/T], percepatan [L/T2], dan gaya [ML/T2].
Bahan Bacaan:
- Sanjoy Mahajan (2010). Street-Fighting Mathematics: The Art of Educated Guessing and Opportunistic Problem Solving. The MIT Press, London.
- Dimensional Analysis, artikel Wikipedia. https://en.wikipedia.org/wiki/Dimensional_analysis
Penulis:
Theodorus Permana, mahasiswa S-3 di Departemen Geofisika, Tohoku University, Jepang.
Kontak: theodorus.permana(at)gmail(dot)com.



