Dalam pelajaran termodinamika, kita telah mengenal konsep mesin kalor sebagai alat yang dapat mengubah energi panas menjadi energi mekanik. Sebagai contoh, mesin mobil mengubah energi panas hasil pembakaran bahan bakar menjadi energi gerak mobil. Akan tetapi, dalam semua mesin kalor kita ketahui bahwa tidak semua energi panas dapat seutuhnya diubah ke energi mekanik.
Perhatikan gambar ilustrasi mesin kalor. Jika kita mengalirkan kalor dari reservoir panas bersuhu T_H ke reservoir dingin bersuhu T_C, usaha sebesar W dapat diekstrak oleh sistem mesin yang muncul dari perbedaan kalor reservoir panas Q_H dan kalor yang ditransfer ke reservoir dingin Q_C.
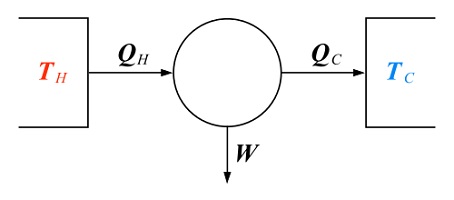
Berdasarkan konservasi energi, kita dapat menuliskan
Q_H = W + Q_C,
atau
W = Q_H - Q_C.
Secara naif, kita mungkin berpikiran usaha dapat diperoleh dari Q_H sepenuhnya (100%) jika ditetapkan Q_C. Pada kenyataannya, akan selalu ada nilai Q_C berupa panas yang diambil dari sistem sebagai akibat dari mesin kalor yang perlu melakukan suatu siklus termodinamika tertentu. Oleh karena itu, dapat didefinisikan efisiensi mesin kalor \eta sebagai nilai usaha yang dapat diekstrak dibagi dengan kalor Q_H yang diberikan pada sistem:
\eta = \displaystyle \frac{W}{Q_H}.
Pada tahun 1824, Sadi Carnot menyusun suatu siklus termodinamika reversibel yang terdiri dari beberapa tahap yang akan menghasilkan nilai efisiensi maksimum. Proses reversibel merupakan proses yang dapat terjadi bolak-balik dan merupakan suatu kondisi ideal. Carnot lantas berhipotesis bahwa tidak ada mesin kalor yang dapat melebihi efisiensi maksimum tersebut. Belakangan, Rudolf Clausius pada tahun 1850 dapat membuktikan hipotesis Carnot melalui pendekatan hukum termodinamika kedua dengan mendefinisikan variabel entropi S sebagai kalor per temperatur, yakni S = Q / T.
Penurunan sederhana untuk efisiensi mesin kalor yang berbasis pada siklus Carnot dapat dijabarkan sebagai berikut:
\eta = \displaystyle\frac{W}{Q_H} = \displaystyle\frac{Q_H - Q_C}{Q_H} = 1 - \displaystyle\frac{Q_C}{Q_H}.
Untuk suatu proses yang reversibel, Clausius menyatakan bahwa S_H = S_C sehingga
\displaystyle\frac{Q_H}{T_H} = \displaystyle\frac{Q_C}{T_C},
atau
\displaystyle\frac{Q_C}{Q_H} = \displaystyle\frac{T_C}{T_H}.
Kondisi siklus mesin kalor yang reversibel ini merupakan kondisi ideal, yang berarti bahwa efisiensi yang dihasilkannya adalah efisiensi maksimum. Jika kita masukkan hubungan Q_C / Q_H ke dalam rumusan efisiensi, kita dapatkan:
\eta_\textrm{max} = 1 - \displaystyle\frac{T_C}{T_H}.
Jadi, pada dasarnya untuk setiap mesin kalor di kehidupan nyata yang bersifat tidak reversibel (yang dalam hal ini berlaku Q_H / T_H < Q_C / T_C atau S_H < S_C) nilai efisiensi maksimum yang bisa dicapai pun bukan 100%, melainkan jauh di bawah itu yang ditentukan oleh rasio T_C / T_H sesuai teorema Carnot dan Clausius. Bahkan, kenyataannya sampai saat ini tidak ada mesin yang mampu mencapai efisiensi maksimum \eta_\textrm{max} = 1 - T_C / T_H.
Hukum-hukum termodinamika dasar yang membatasi efisiensi mesin kalor ini telah menggelitik cukup banyak fisikawan pada abad ke-19 dan 20. Perdebatan hangat masih sering terjadi dalam tataran fundamental untuk lebih memahami konsep kalor, usaha, dan entropi. Di antara perdebatan itu sempat muncul beberapa ide dan percobaan yang mengkaji kemungkinan membuat mesin kalor “abadi”, yaitu mesin kalor yang dapat menghasilkan usaha terus-menerus.
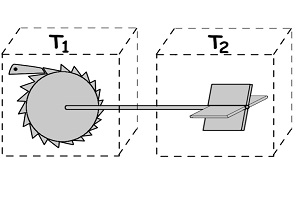
Salah satu percobaan pikiran (percobaan yang tidak benar-benar direalisasikan, hanya dibayangkan saja) yang cukup menarik untuk dibahas di sini adalah mesin kalor berbasis gerak Brown. Gerak Brown adalah gerak acak partikel yang berada di dalam suatu gas atau cairan sebagai akibat tumbukannya satu sama lain. Perhatikan ilustrasi. Pada tahun 1912, seorang fisikawan Polandia bernama Marian Smoluchowski mengajukan percobaan pikiran bahwa mungkin saja mesin kalor dihasilkan dari gerak Brown jika reservoir panas bersuhu T_1 dan reservoir dingin bersuhu T_2 berisi gas pada suhu yang berbeda, yakni T_1 > T_2.
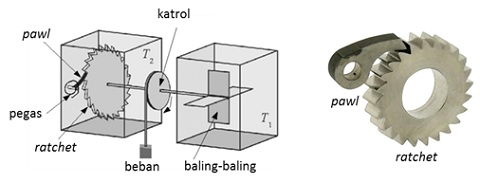
Mesin kalor berbasis gerak Brown ini memiliki baling-baling di dalam reservoir panas dan pasangan ratchet–pawl di dalam reservoir dingin. Ratchet dan pawl merupakan suatu sistem gerigi yang memungkinkan perputaran hanya pada satu arah saja. Ratchet terbuat dari sebuah roda gerigi yang gigi-giginya asimetris mengarah pada arah tertentu. Pawl adalah suatu tangkai yang mengait pada roda gerigi ratchet dan biasanya disertai sebuah pegas untuk menjamin pergerakan ratchet hanya pada satu arah saja (misalnya searah jarum jam saja seperti pada gambar).
Hal yang menarik dari mesin kalor Smoluchowski adalah penggunaan percobaan pikiran tersebut untuk membantah kemungkinan adanya mesin kalor abadi yang hanya mengandalkan gerak Brown tanpa adanya perpindahan kalor (dalam hal ini, T_1 = T_2). Pada kondisi T_1 = T_2, bayangkan tumbukan molekul gas akan menyebabkan baling-baling berguncang. Ketika baling-baling mencoba untuk berputar pada satu arah tertentu yang tidak diizinkan sistem ratchet–pawl, maka baling-baling tersebut tidak akan bergerak. Namun, jika molekul-molekul gas menumbuk baling-baling pada arah lain yang diizinkan sistem ratchet-pawl, apakah ada kemungkinan gerigi ratchet dan katrol bersama bebannya ikut bergerak? Jika iya, usaha W dapat dihasilkan pada T_1 = T_2 , dan hal ini menjadi paradoks yang melanggar hukum termodinamika.
Richard Feynman pada tahun 1962 memopulerkan percobaan pikiran Smoluchowski pada serial kuliah fisika dasar beliau (Feynman’s Lectures in Physics) dan memberikan penjelasan kuantitatif berdasarkan distribusi Maxwell-Boltzmann mengenai apa yang akan terjadi pada mesin kalor berbasis gerak Brown tersebut. Misalkan energi pawl untuk melawan pegas (sehingga roda ratchet dapat berputar adalah E. Pada kondisi T_1 = T_2 = T, peluang sistem dapat mengakumulasi cukup energi E untuk memutar gerigi ratchet dari hasil gerak Brown pada baling-baling adalah \exp(-E/kT), dengan k merupakan konstanta Boltzmann. Akan tetapi, kita dapat lihat bahwa kemungkinan pawl secara tidak sengaja terangkat juga sama saja dengan \exp(-E/kT).
Berdasarkan argumen Feynman tersebut, kita dapat simpulkan bahwa peluang pawl terangkat dan katrol berputar melawan jarum jam sebanding dengan jumlah energi yang dibutuhkan untuk memutar katrol searah jarum jam saat ratchet bergerak di satu arah yang diizinkan. Dari sini kita dapatkan keseimbangan dan katrol memang tidak akan berputar. Dengan demikian, hukum termodinamika tidak terlanggar dan paradoks dapat terpecahkan. Mustahil untuk membuat mesin kalor bekerja pada kondisi T_1 = T_2.
Lalu, apa yang terjadi jika T_1 > T_2 pada mesin kalor Smoluchowski? Sesuai hipotesis Smoluchowski, Feynman dapat pula menunjukkan secara kuantitatif bahwa sangat mungkin menghasilkan usaha pada kondisi tersebut. Dengan kata lain, mesin kalor tersebut dapat “berguna”. Di bawah ini kita akan menguraikan argumen Feynman untuk T_1 > T_2.
Asumsikan sistem dapat bergerak pada arah normal sesuai dengan pola gerigi ratchet. Untuk membuat katrol bergerak sejauh satu gigi, energi yang harus diambil dari baling-baling untuk ratchet adalah sebesar E. Gerigi ratchet akan bergerak sejauh sudut \theta dan melawan momen gaya sebesar L. Misalkan kalor yang dibutuhkan adalah Q_1, prinsip konservasi energi yang berlaku adalah
Q_1 = E + L \theta,
sehingga peluang untuk mendapatkan energi sebesar itu sesuai distribusi Maxwell-Boltzman akan sebanding dengan
\exp \left(- \displaystyle\frac{E + L\theta}{kT_1} \right).
Jika kita meninjau berapa kali sistem per detiknya dapat memiliki Q_1, kita bisa pula masukkan konstanta waktu 1/\tau sehingga laju peluang pergerakan katrol searah jarum jam adalah
\exp \left(- \displaystyle\frac{E + L\theta}{kT_1} \right) \times \displaystyle\frac{1}{\tau}.
Selanjutnya, kita tinjau gerakan yang berlawanan dengan arah pola gerigi ratchet (berlawanan jarum jam seperti pada ilustrasi). Untuk membuat katrol bisa bergerak berlawanan jarum jam, dibutuhkan energi yang cukup untuk mengangkat pawl, yaitu E. Nilai E ini setara dengan kalor yang dilepaskan dalam proses tersebut (Q_2), yakni Q_2 = E. Dengan demikian, laju peluang pergerakan katrol berlawanan jarum jam adalah
\exp \left(- \displaystyle\frac{E}{kT_2} \right) \times \displaystyle\frac{1}{\tau}.
Sekarang andaikan sistem mesin kalor Smoluchowski bersifat reversibel. Asumsi ini mengakibatkan peluang katrol bergerak searah jarum jam akan sama dengan peluang gerak yang berlawanan,
\exp \left(- \displaystyle\frac{E + L\theta}{kT_1} \right) \times \displaystyle\frac{1}{\tau} = \exp \left(- \displaystyle\frac{E}{kT_2} \right) \times \displaystyle\frac{1}{\tau}.
Kita sederhanakan sedikit persamaan ini, hasilnya adalah
\displaystyle\frac{E+L\theta}{T_1} = \displaystyle\frac{E}{T_2}
\displaystyle\frac{Q_1}{T_1} = \displaystyle\frac{Q_2}{T_2},
atau Q_2 / Q_1 = T_2 / T_1. Perhatikan bahwa persamaan yang terakhir ini merupakan ungkapan yang serupa dengan dengan perbandingan kalor dalam efisiensi maksimum mesin Carnot. Artinya, mesin kalor berbasis gerak Brown ini mungkin memiliki efisiensi yang sama idealnya dengan mesin Carnot yakni:
\eta = 1 - \displaystyle\frac{Q_2}{Q_1},
sehingga
\eta_\textrm{max} = 1 - \displaystyle\frac{T_2}{T_1}.
Sementara itu, untuk proses yang tidak reversibel (kondisi nyata yang tidak ideal), dapat dituliskan lagi hubungan Q_2 / Q_1 < T_2 / T_1 sehingga Q_2 / T_2 < Q_1 / T_1. Dengan kata lain, entropi S_2 < S_1. Argumen Feynman ini turut membuktikan bahwa tidak ada mesin yang mampu melampaui efisiensi sebesar mesin Carnot yang mengandung proses reversibel. Andaikata ada, itu akan melanggar hukum termodinamika sehingga menjadi kontradiksi yang tidak mungkin terjadi.
Sebagai catatan akhir, meskipun argumen Feynman tampak “benar”, pada rentang tahun 1996-2000, Juan Parrondo menunjukkan beberapa kesalahan analisis Feynman. Di antaranya, Parrondo menyatakan bahwa mesin kalor berbasis gerak Brown ini tidak pernah mungkin bisa reversibel karena dua reservoir pada temperatur yang berbeda selalu dihubungkan langsung oleh tuas yang memanjang dari baling-baling ke gerigi ratchet. Meskipun demikian, konsep mesin kalor berbasis gerak Brown ini cukup bermanfaat telah merangsang dan menginspirasi penemuan beberapa konsep baru pada nanoteknologi dan bahkan ekonomi, seperti Brownian motor dan ratchet effect.
Bahan bacaan:
- http://www.feynmanlectures.caltech.edu/I_46.html
- https://en.wikipedia.org/wiki/Brownian_ratchet
- https://en.wikipedia.org/wiki/Brownian_motor
- https://en.wikipedia.org/wiki/Ratchet_effect
- M. R. Parrondo dan P. Espanol, Criticism of Feynman’s analysis of the ratchet as an engine, Am. J. Phys. 64, 1125 (1996): http://dx.doi.org/10.1119/1.18393
Penulis:
- Akhmad Yulianto, Karyawan Pasadena Engineering Indonesia, alumnus ITB dan KTH Swedia.
Kontak: akhmadyulianto(at)gmail(dot)com. - Ahmad Ridwan T. Nugraha, peneliti fisika, alumnus ITB dan Tohoku University.
Kontak: art.nugraha(at)gmail(dot)com.