Model Fisika Sederhana untuk Bersin

Seiring pandemi Covid-19, beberapa daerah di Indonesia memberlakukan pembatasan sosial berskala besar (PSBB) untuk mencegah penyebaran virus korona SARS-CoV-2. Beberapa poin dari PSBB tersebut adalah kewajiban menggunakan masker dan menjaga jarak dengan orang lain (physical distancing) sekurang-kurangnya 2 meter. Salah satu alasan dari menjaga jarak tersebut adalah untuk menghindari penularan virus melalui aerosol yang keluar ketika seseorang bersin karena aerosol dapat menjadi media penyebaran virus korona.

Dalam tulisan ini, mari kita bahas model fisika sederhana untuk menjelaskan fenomena bersin. Model yang akan kita gunakan adalah kinematika gerak parabola. Teman-teman pernah belajar tentang gerak parabola di sekolah, bukan? Gerak parabola adalah gerak dua dimensi yang lintasan bendanya berbentuk parabola. Gerak ini merupakan perpaduan antara gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB).

Jangan lupa, GLB adalah gerak lurus dengan kecepatan tetap, sedangkan GLBB adalah gerak benda dengan percepatan tetap yang artinya kecepatan benda berubah secara beraturan. Dalam model ini, kita mengasumsikan bahwa aerosol yang ke luar ketika sesorang bersin mematuhi kinematika benda titik pada fisika.

Berdasarkan penelitian yang dilakukan oleh Tang, dkk. pada April 2013, rata-rata kecepatan aerosol ketika seseorang bersin adalah 4,5 m/s. Dengan mengasumsikan tinggi mulut dari permukaan tanah adalah 1,6 meter, kita dapat menentukan seberapa jauh aerosol akan bergerak saat seseorang bersin tanpa menggunakan masker.

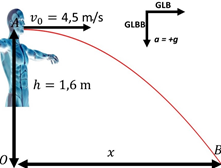
Ilustrasi lintasan aerosol ketika seseorang bersin.

Dalam gerak parabola, gerak ke arah horizontal adalah GLB dan gerak ke arah vertikal adalah GLBB dengan percepatan sebesar percepatan gravitasi. Sudut yang dibentuk antara arah horizontal dengan lintasan awal aerosol (θ) adalah 0 (nol). Ingat sin 0^o = 0 dan cos 0^o = 1. Proyeksi dari kecepatan partikel pada masing-masing sumbu dapat dituliskan:

v_x = v_{0x} = v_0 \cos \theta = 0

v_{0y} = v_0 \sin \theta = 0

v_y = v_{0y} + at = gt

Jarak vertikal yang akan ditempuh oleh aerosol adalah

y = v_{0y} t + \frac{1}{2} gt^2

h = \frac{1}{2} g t^2

Dengan menggunakan rumus tersebut, kita bisa menghitung waktu yang dibutuhkan oleh aerosol dari mulut (titik A) untuk sampai ke tanah (titik B):

$t_{AB} = \displaystyle \sqrt{\frac{2h}{g}}$ .

Waktu tempuh (t_AB) digunakan untuk menghitung jarak horizontal yang ditempuh aerosol sebelum jatuh ke lantai, yakni:

x = v_x t_{AB}

x = \displaystyle v_x\sqrt{\frac{2h}{g}}

x = \displaystyle 4,5 \sqrt{\frac{2(1,6)}{9,8}} \textrm{m} = 2,57~\textrm{m}

Berdasarkan perhiungan di atas, maksimum jarak horizontal adalah 2,57 m. Ketika kita menjaga jarak setidaknya 2 m dari orang lain, diharapkan virus yang dibawa oleh aerosol dari semburan bersin tidak kita hirup karena posisi aerosol akan jauh dari hidung kita atau kira-kira sekitar 63 cm dari lantai.

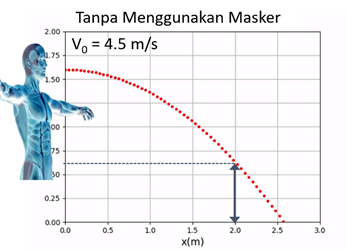
Grafik lintasan aerosol ketika seseorang bersin.

Model kinematika yang kita gunakan untuk memodelkan bersin merupakan model yang sangat sederhana karena kita tidak mempertimbangkan aliran udara dan faktor-faktor lain. Namun, model ini dapat menjelaskan mengapa kita perlu menjaga jarak minimal 2 m saat PSBB.

Bahan bacaan:

Tang, Julian W., et al. “Airflow dynamics of human jets: sneezing and breathing-potential sources of infectious aerosols.” PLoS One4 (2013).

Penulis:
Syahril Siregar, peneliti fisika komputasi dan biofisika di Lund University, Swedia.
Kontak: syahril.deutch(at)gmail(dot)com.

Model Fisika Sederhana untuk Bersin