Peran Matematika dalam Ilmu Forensik

Teman-teman mungkin pernah menonton film-film detektif, baik film berjenis kartun maupun film yang diangkat dari kisah nyata seperti CSI Files dan Forensic Files. Kalau teman-teman perhatikan, kasus yang paling sering ditampilkan dalam film maupun kisah nyata adalah kasus penemuan jenazah. Dalam film-film tersebut seorang detektif dan ahli forensik dapat menentukan kapan jenazah tersebut meninggal dunia.

Penentuan perkiraan kapan korban meninggal dunia sangat penting dalam menentukan siapa pembunuh korban. Pada kesempatan kali ini, kita akan membahas bagaimana cara detektif dan ahli forensik menentukan waktu kematian korban dengan menggunakan hukum pendinginan Newton. Hukum ini ditemukan oleh Sir Isaac Newton, ilmuwan yang sama dengan penemu hukum tentang gerak.

Manusia merupakan makhluk berdarah panas. Artinya, suhu tubuh manusia tidak banyak dipengaruhi suhu lingkungan. Suhu tubuh manusia normal adalah 37,5 ^oC. Pada saat seseorang meninggal, suhu tubuhnya tidak akan 37,5 ^oC, tetapi turun secara perlahan sehingga dalam jangka waktu tertentu suhunya akan sama dengan suhu lingkungan. Dalam hal ini, suhu lingkungan dianggap lebih rendah dari suhu tubuh manusia normal. Pada umumnya, suhu lingkungan adalah 27 ^oC.

Proses penurunan suhu pada tubuh manusia ketika mengalami kematian ternyata mengikuti hukum pendinginan Newton. Hukum ini mengatakan bahwa penurunan suhu suatu benda yang memiliki suhu lebih tinggi dari lingkungannya berbanding lurus dengan selisih suhu benda tersebut dengan lingkungannya. Secara matematis, hukum pendinginan Newton dapat ditulis menjadi

$\displaystyle\frac{dT}{dt} = -k(T - T_a)$

Pada rumus di atas, dT/dt adalah perubahan suhu terhadap waktu, k adalah suatu konstanta dengan satuan 1/waktu, T adalah suhu benda sebagai fungsi waku dan T_a adalah suhu lingkungan. Nilai konstanta k dapat ditentukan dengan mengukur suhu pada waktu yang berbeda, tetapi untuk tubuh manusia pada umumnya adalah 0,696/jam. Kita dapat menyelesaikan persamaan di atas dengan melakukan proses integral sederhana:

$\displaystyle\int\frac{dT}{T - T_a} = -k \int dt$

$\ln |T - T_a = - k t + C$

dengan C adalah suatu konstanta yang dapat ditentukan dengan memasukan suhu awal T_0. Solusi akhir dari persamaan di atas menjadi

$T(t) = T_a + (T_0 - T_a) e^{-k t}$

Setelah berhasil menurunkan persamaan di atas, mari kita tinjau contoh kasus nyata. Dalam kasus pembunuhan ditemukan mayat di dalam rumah dengan suhu tubuh 28 ^oC dan suhu di dalam rumah pada saat itu 27 ^oC. Mayat ditemukan pada hari Selasa pukul 16:00. Kapan pembunuhan itu dilakukan?

Dari kasus ini, kita dapat menentukan beberapa besaran: T(t) = 28 ^oC, T_o = 37,5 ^oC, dan T_a = 27 ^oC. Dengan mensubstitusi besaran-besaran tersebut ke dalam persamaan hukum pendinginan Newton, akan didapatkan hasil sebagai berikut

$28 = 27 + (37,5 - 27)e^{-0,696 t}$

$1 = 10,5 e^{-0,696 t}$

$t = \displaystyle \frac{\ln (10,5)}{0,696}$

$t = 3,38~\textrm{jam} = 3~\textrm{jam}~22~\textrm{menit}$

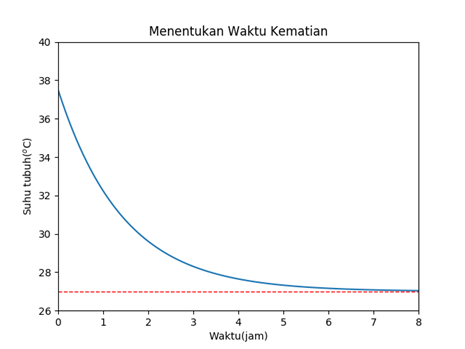
Jika kita kurangi waktu penemuan mayat dengan hasil perhitungan, perkiraan waktu kematian korban adalah hari Selasa pukul 12:38. Pada dapat dilihat hasil perhitungan penurunan suhu tubuh manusia setelah kematian selama 8 jam. Garis merah menunjukkan suhu lingkungan 27 ^oC. Bagaimana? Teman-teman tertarik menjadi detektif? Ilmu matematika dan fisika ternyata cukup bermanfaat bagi para detektif!

Kurva penurunan suhu tubuh terhadap waktu.

Bahan bacaan:

Penulis:
Syahril Siregar, Mahasiswa S-3 di Graduate School of Biomedical Engineering, Tohoku University, Jepang.
Kontak: syahril.deutch(at)gmail(dot)com.

Peran Matematika dalam Ilmu Forensik