Pernahkan kalian memperhatikan pilar di rumahmu, rumah tetangga, atau di supermarket? Bagaimanakan bentuk pilar yang dibuat? Beberapa bangunan menggunakan pilar berbentuk tabung, misalnya bangunan kuno di Yunani yang terkenal dengan nama The Phartenon. Beberapa bangunan menggunakan bentuk lain seperti balok, misalnya di kebanyakan rumah kita.

Sumber gambar dari Google Search.
Sebenarnya mana yang lebih kuat, pilar yang berbentuk tabung atau balok untuk menahan beban genteng jika luas permukaan tabung dan balok itu sama? Untuk dapat menjawab ini kita dapat melakukan percobaan sederhana dari kertas. Kegiatan ini diperagakan dua orang guru matematika yaitu Novita Vindri dari Jawa Timur (Indonesia) dan Ong Khye Ching dari Sabah (Malaysia), saat keduanya mengikuti pelatihan SEA RME untuk guru matematika SMP.
Berikut ini adalah langkah-langkah yang akan kita lakukan.
- Ambil 2 lembar kertas A4.
- Satu lembar kertas dibentuk menjadi balok dan satu lembar yang lain dibentuk menjadi tabung dengan bantuan double tape, keduanya tanpa alas dan tutup seperti pada gambar di bawah ini.

- Untuk mengetahui mana yang lebih kuat menahan beban, kita meletakkan beban berupa buku di atas balok dan tabung.

- Hasil percobaan menunjukkan ternyata balok tidak kuat menahan beban. Meski demikian, tabung lebih kuat menahan beban bahkan setelah diberi tambahan beban.

Kita bisa menganalisis secara sederhana mengapa pilar tabung bisa menahan beban lebih baik daripada pilar balok. Beban yang datang kepada balok tanpa tutup hanya tersebar kepada empat titik/tempat saja, yaitu pada pojok-pojoknya, sedangkan pada tabung tanpa tutup, beban yang datang disebarkan secara merata pada setiap titik pada lingkaran atas.
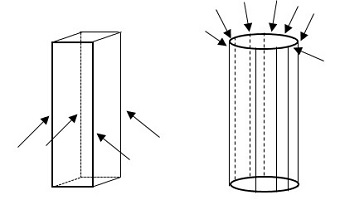
Untuk ukuran kertas yang sama, didapat keliling persegi = keliling lingkaran. Untuk keliling yang sama, luas penampang tabung yang berbentuk lingkaran lebih luas daripada luas penampang balok yang berbentuk persegi. Semakin besar luas penampang, bangun ruang dapat menahan semakin berat beban. Inilah yang mengakibatkan tabung mampu menahan beban tersebut daripada balok tersebut.
Pembelajaran sederhana ini dapat kita sampaikan untuk permulaan pada pembelajaran balok dan tabung untuk memotivasi siswa bahwa matematika berguna untuk kehidupan sehari-hari.
Catatan:
- Tulisan ini terinspirasi dari ulasan Bapak Hery Sutarto di: http://www.prioritaspendidikan.org/id/post/380
- SEA RME adalah South East Asia Realistic Mathematics Education for Secondary High School Mathematics Teacher, yang diselenggarakan oleh SEAMEO for QITEP di PPPPTK Matematika Yogyakarta, 17-30 Mei 2016.
Penulis:
Eny Susiana, Guru Matematika SMPN 1 Jakenan, Kab Pati, Jawa Tengah.
Kontak: enysusiana(at)gmail(dot)com.



