Ketika Jarak Terdekat Tidak Selalu Garis Lurus

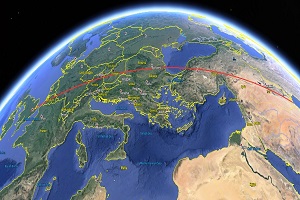
“Ambil selembar kertas dan gambarlah buah dua titik,” perintah ibu guru kepada para murid di kelas. Budi kecil dengan antusias melakukan apa yang diperintahkan sang guru. “Berilah nama A pada salah satu titik dan B pada titik yang lain,” lagi perintah ibu guru. “Berbentuk apakah jarak terpendek titik A ke titik B?”

Dengan sedikit berpikir, Budi kecil kemudian mengacungkan tangan. “Garis lurus!” seru Budi. “Ya, seratus untuk Budi!” puji ibu guru. Itulah kenangan yang diingat Budi ketika belajar matematika geometri di sekolah dasar.

Namun Budi yang telah menjadi dewasa kini terperangah ketika melihat aplikasi Google Maps. Iseng-iseng dia ingin menghitung jarak terdekat antara Fortaleza di Brazil dan Jakarta di Indonesia. Beginilah yang didapatkannya.

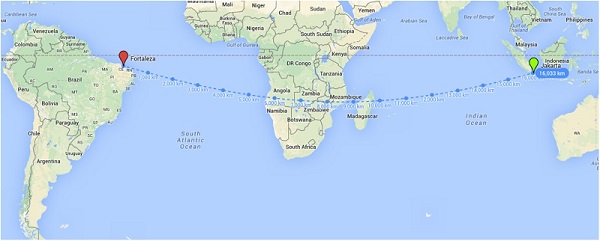
Pertama, jarak terdekat Jakarta-Fortaleza adalah 16033 km. Kedua, ternyata jarak terdekat antara kedua kota tidaklah berbentuk garis lurus! Kalau kita paksakan menggunakan garis lurus yang ‘sejajar’ dengan jarak kedua kota, kita akan mendapatkan jarak sekitar 16183 km, atau 150 km lebih jauh daripada pengukuran pertama.

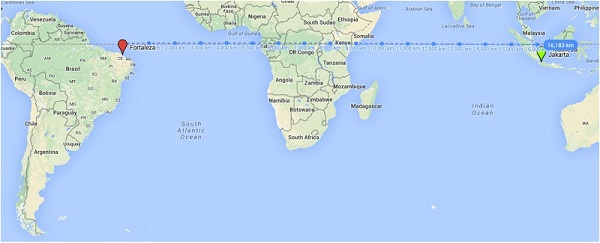
Mengapa demikian? Perlu diingat bahwa gambar dua dimensi peta di atas merupakan proyeksi Mercator yang tidak tepat dalam menggambarkan bola dunia sesungguhnya. Untuk mengetahui bagaimana mengukur jarak terdekat pada permukaan bola kita perlu mempelajari lebih dalam seputar koordinat bola.

Pada majalah 1000guru rubrik matematika edisi September 2014, kita telah belajar dari Kak Gian bahwa geometri bola berbeda dengan geometri Euklidean, semacam kertas maupun papan tulis. Bila kita menggambar segitiga pada kertas, sudut total yang dibentuk oleh ketiga titik sudut adalah 180 derajat. Namun, bila kita menggambar segitiga di permukaan bola, kita akan mendapati bahwa sudut yang dibentuk lebih dari 180 derajat! Di atas kertas mendatar, jarak terdekat antara dua titik  A dan B (sebutlah sebagai d_AB) berbentuk garis lurus, sedangkan di permukaan bola tentunya berbentuk garis busur permukaan bola.

Panjang busur lingkaran dan konsep radian

Sebelum mempelajari geometri bola, mari kita belajar geometri yang lebih sederhana, yaitu lingkaran. Mari kita ambil irisan lingkaran AOB berikut.

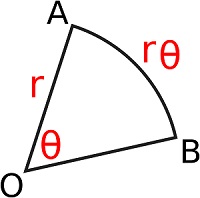
Bila sudut θ adalah sudut AOB yang dinyatakan dalam radian dan panjang jari-jari lingkaran adalah r, panjang busur AOB adalah rθ. Kita dapat dengan mudah mengonversi satuan sudut dalam radian menjadi derajat melalui keliling lingkaran.  Perhatikan bahwa keliling lingkaran adalah 2πr = rθ, kemudian θ = 2π radian = 360^o. Dengan demikian, 1 radian setara 180^o/π .

Jarak antara dua titik dalam koordinat bola

Pertama, kita misalkan bahwa Bumi berbentuk bulat penuh. Setiap titik dalam koordinat bola Bumi ditentukan oleh sudut lintang θ, sudut bujur φ, dan τ = 90^o – θ = π/2 – θ (dalam radian).

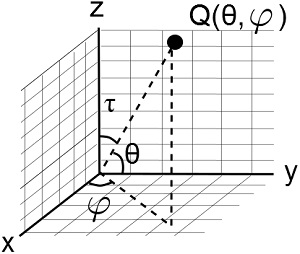
Perlu diketahui bahwa konvensi sudut yang digunakan dalam koordinat bola Bumi sedikit berbeda dengan koordinat bola pada umumnya. Dalam koordinat Bumi, kita membagi belahan Bumi utara dan selatan sehingga garis lintang θ diukur dari sumbu-xy, sedangkan dalam koordinat bola pada umumnya θ diukur dari sumbu-z (dalam hal ini τ).

Sekarang kita letakkan dua titik, yaitu A (θ_A, φ_A) dan B (θ_B, φ_B) di permukaan bola.

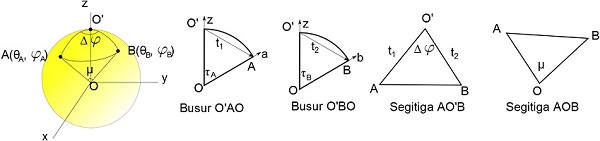
Sudut antara titik A dan B diukur dari pusat bola adalah µ. Maka, jarak AB di permukaan bola adalah d_AB = rµ, dengan r adalah jari-jari Bumi. Tugas kita sekarang adalah mencari nilai µ dengan analisis vektor.

Kita dapat memecah permasalahan 3 dimensi ini untuk mendapatkan busur O’AO dan O’BO. Di dalam busur O’AO terdapat vektor satuan z pada garis OO’, vektor satuan a pada garis OA, serta vektor satuan t₁ yang menghubungkan z dan a menjadi segitiga O’AO. Vektor satuan adalah vektor yang bernilai satu sehingga berlaku perkalian titik:

\mathbf{a \cdot z =\left | a \right |\left | z \right |}\cos\tau_A = \cos \tau_A

Vektor satuan t₁ didapatkan dengan analisis trigonometri pada segitiga O’AO,

\mathbf{t_1} \sin\tau_A = \mathbf{a} - \mathbf{z} \cos\tau_A

Dengan cara yang sama, kita akan mendapakan t₂ untuk segitiga O’BO,

\mathbf{t_2} \sin\tau_B = \mathbf{b} - \mathbf{z} \cos\tau_B

t₁ dan t₂ adalah vektor yang kita perlukan untuk membuat segitiga AO’B. Hubungan t₁ dan t₂ terhadap µ didapatkan melalui hubungan perkalian titik

\cos(\Delta \varphi) = \mathbf{t_1 \cdot t_2} = \frac{ ( \cos\mu - \cos\tau_A \cos\tau_B )}{ ( \sin\tau_A \sin\tau_B ) }

dengan Δφ = φ_A – φ_B.  Dalam perkalian titik di atas, perlu diketahui bahwa a . b = cos µ. Melalui hubungan τ = π/2 – θ, kita peroleh cos τ = sin θ dan sin τ = cos θ. Dari persamaan di atas kita mendapatkan nilai µ sebagai,

\mu = \cos^{-1} ( \sin\theta_A \sin\theta_B + \cos\theta_A \cos\theta_B \cos\Delta\varphi )

Oleh sebab itu, jarak AB di  permukaan bola diberikan oleh

d_{AB} = r\cos^{-1} ( \sin\theta_A \sin\theta_B + \cos\theta_A \cos\theta_B \cos\Delta\varphi )

Menurut Google Maps, koordinat Jakarta (kita anggap sebagai kota A) adalah

θ_A = 6°10’14.4″ lintang selatan (LS) = 6.170667° LS = 0.107698456 radian LS,

φ_A = 106°49’37.7″ bujur timur (BT) = 106.8269° BT = 1.86448113 radian BT

dan Fortaleza (kita anggap sebagai kota B) adalah

θ_B = 3°43’54.6″ LS =  3.731833° LS = 0.065132773 radian,

φ_B = 38°31’34.8″ bujur barat (BB) =  38.52633° BB = 0.672411307 radian BB = – 0.672411307 radian BT.

Jari-jari Bumi diketahui sebesar 6371 km.

Dengan memasukkan parameter-parameter di atas ke dalam rumus d_AB, kita dapatkan d_AB = 16065 km. Hasil yang cukup mendekati dari perkiraan Google Maps, yaitu 16033 km. Sekarang dengan rumus di atas, kalian dapat menghitung sembarang jarak antara dua titik di permukaan bola dunia. Cobalah cari berapakah jarak antara kotamu dengan London? Dan carilah di manakah titik terjauh di permukaan bola Bumi diukur dari kotamu, serta tentukan jaraknya.

Bahan bacaan:

• https://en.wikipedia.org/wiki/Great-circle_distance
• https://en.wikipedia.org/wiki/Spherical_law_of_cosines
• http://majalah1000guru.net/2014/09/mengenal-geometri-bola/

Penulis:
Eddwi Hesky Hasdeo, peneliti fisika, alumnus Universitas Brawijaya dan Tohoku University, Jepang.
Kontak: heskyzone(at)gmail(dot)com