Paradoks Terompet Torricelli

Tet… Toet… Tet… Toet… Wah, ada bunyi terompet! Biasanya pada perayaan tertentu anak kecil maupun orang dewasa suka meniup terompet. Nah, tahukah teman-teman? Ada suatu paradoks yang menarik tentang terompet yang dikenal dengan istilah paradoks terompet Jibril, atau terompet Torricelli, sesuai dengan pencetusnya yang bernama Evangelista Torricelli. Terompet ini memiliki volume yang terbatas (finite) dengan luas yang tidak terbatas (infinite).

Bagaimana terompet Torricelli bisa terbentuk? Sebelum menghitung luas terompet ini, kita harus tahu dulu bagaimana cara menghitung luas permukaan di bawah kurva. Dulu, di saat Newton dan Leibniz belum menemukan teori integral, cara yang digunakan untuk menghitung luas di bawah kurva adalah dengan membagi daerah menjadi persegi-persegi kecil yang memiliki tinggi f(x_i) dan lebar Δx_i. Persegi ini dihitung luasnya, kemudian dijumlahkan seluruhnya.

Perhatikan gambar, kita bisa tuliskan luas area di bawah kurva sebagai

$A = f(x_1) \Delta x_1 + f(x_2) \Delta x_2 + \cdots + f(x_n) \cdot \Delta x_n$

Kita asumsikan bahwa Δx_i bernilai sama untuk setiap persegi sehingga Δx₁ = Δx₂ = Δx_n. Untuk nilai n menuju tak hingga, maka nilai Δx_n akan menuju nol. Dengan demikian, ekspresi luas di bawah kurva dapat kita tuliskan menjadi:

$A = \lim_{n \to \infty } \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i = \lim_{x \to 0} \sum_{x = a}^{b} f(x_i)\cdot\Delta x_i$

Atau, menurut teori Newton dan Leibniz kita dapat menyederhanakannya menjadi:

$A = \int_{a}^{b} f(x)dx$

Jika suatu kurva memiliki fungsi f(x) = 3x², dengan batas atas b = 4 dan batas bawah a = 2, secara ringkas kita bisa mendapatkan luas area di bawah kurva sebesar :

$A = \int_{2}^{4} 3x^{2} dx = [x^{3}]_2^4 = 56$

Nah, coba kalau kita mempunyai luas daerah di bawah dua kurva, yaitu:

$f(x) = 4x^{2} - x$

dan

$g(x) = 5x^{3}$

Berapa luas daerah yang kita miliki? Coba teman-teman cari solusinya sendiri untuk bahan latihan, ya.

Sekarang, kita tinjau paradoks terompet Torricelli. Untuk keperluan ini, kita gambarkan kurva f(x) = 1/x pada domain [0, ∞] yang kita putar pada sepanjang sumbu x sehingga menghasilkan suatu permukaan seperti pada gambar.

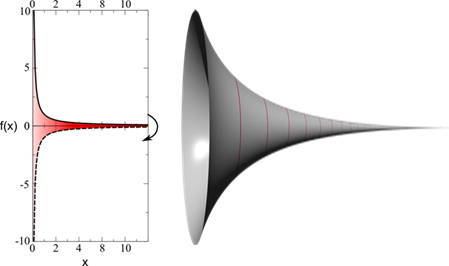
Seperti disebutkan di awal, terompet ini memiliki volume yang terhingga dengan luas permukaan yang tak terhingga. Mari kita buktikan dengan menghitung volume:

$V = \int_{1}^{\infty} \pi \left ( \frac{1}{x} \right )^{2}\ dx = \lim_{ b \to \infty } \int_{1}^{b} x^{-2}\ dx = \lim_{ b \to \infty } \left [ \frac{ - \pi }{x} \right ]_{1}^{b} = \pi \approx 3.141592 \cdots$

Sementara itu, untuk luasnya bisa kita hitung sebagai berikut:

$A = \int_{1}^{\infty} 2 \pi y\ ds = \int_{1}^{\infty} 2\pi y \sqrt{1+ \left ( \frac{dy}{dx} \right )^{2}}\ dx = 2 \pi \int_{1}^{\infty} \frac{1}{x} \sqrt{1 + \left ( \frac{-1}{x^{2}} \right )^{2}}\ dx$

$A = \lim_{ b \to \infty } 2 \pi \int_{1}^{b} \frac{ \sqrt{x^{4} + 1}}{x^{3}}\ dx\ \cdots (\ast)$

Kita dapat menyederhanakannya dengan kondisi:

$\frac{ \sqrt{x^{4} + 1}}{x^{3}} > \frac{ \sqrt{x^{4}}}{x^{3}} = \frac{1}{x}$

Subsitusikan ekspresi terakhir ini ke persamaan (*),kita dapatkan :

$A = \int_{1}^{b} \frac{\sqrt{x^{4} + 1}}{x^{3}}\ dx > \int_{1}^{b} \frac{1}{x}\ dx = \ln\ b$

Ingat bahwa b pada awalnya , sehingga ln b yang dihitung sebagai ln ∞ menghasilkan A (luas) dengan nilai yang tak terhingga. Menarik, bukan? Bayangkan ketika kita bisa mengisi penuh terompet Torricelli ini dengan cat sebanyak π (luas), tetapi kita membutuhkan cat yang tidak terhingga banyaknya untuk menutupi permukaan terompet Torricelli. Hmm… apakah mungkin? Silakan dipikirkan.

Bahan bacaan:

Penulis:
Evelyn Pratami Sinaga, Mahasiswi Master di Departemen Fisika, Tohoku University.
Kontak: evelynpratami(at)gmail.com

Paradoks Terompet Torricelli