Pernahkah Anda mengatur jadwal suatu turnamen atau kompetisi? Jika pernah, mungkin Anda akan setuju bahwa mengatur jadwal turnamen tidaklah semudah yang kita bayangkan ketika melihat jadwal tersebut sudah rapi tersusun.
Ada dua format utama yang biasanya digunakan para pengatur jadwal pertandingan olahraga, yaitu (1) sistem gugur dan (2) sistem liga. Selain kedua format ini bisa juga dilakukan variasi seperti sistem setengah kompetisi, yaitu membagi peserta ke dalam grup tertentu kemudian dilanjutkan dengan sistem gugur, biasanya format pertandingan ini sering digunakan pada piala dunia. Mari kita bahas satu per satu cara mengatur jadwal menurut masing-masing dari dua format utama sistem pertandingan ini.
Sistem gugur
Dalam format ini, satu kekalahan sudah cukup untuk mengeliminasi peserta yang kalah tersebut dari turnamen secara keseluruhan. Penjadwalan turnamen dengan sistem gugur relatif mudah dilakukan.
Langkah pertama adalah memperoleh jumlah peserta dalam pangkat 2, yaitu 2, 4, 8, 16, 32, dan seterusnya. Jika jumlah peserta bukan dalam pangkat 2, misalnya ada 20 peserta, kita bisa mengambil 8 peserta untuk melakukan tanding pendahuluan untuk mengambil 4 peserta terbaik sehingga sistem gugur bisa dijalankan dengan 16 peserta.
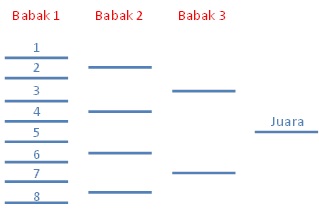
Sistem liga
Dalam format ini, setiap peserta harus melawan setiap peserta lainnya, setidaknya 1 kali, atau 2 kali jika ada home dan away. Ada pendekatan yang cukup sistematis untuk mengatur pertandingan turnamen berformat liga, yang disebut dengan metode poligon. Pendekatan ini mengasumsikan ada sejumlah lapangan yang cukup sehingga seluruh pertandingan pada suatu tahap dapat dilakukan bersamaan.
Pengaturan jadwal turnamen dengan metode poligon tergantung pada jumlah peserta yang mengikuti kompetisi, yaitu jumlahnya genap, atau ganjil. Di sini kita akan bahas jika jumlah pesertanya genap. Jika jumlah pesertanya ganjil, coba pikirkan bagaimana caranya setelah membaca tulisan ini. ;)
Misalkan N adalah jumlah peserta dari suatu turnamen. Dalam kondisi ini akan ada N-1 ronde yang perlu dijalani (misalnya N-1 minggu, jika turnamen diselenggarakan setiap pekan). Setiap tim secara total akan bermain sejumlah N-1 kali. Karena setiap tim akan melawan tim lainnya pada setiap tahap, tidak akan ada tim yang tidak bertanding dalam setiap tahapnya.
Mari kita atur jadwal pertandingan dari suatu turnamen yang melibatkan 8 peserta yang diberi nomor 1 s.d. 8. Langkah pertama, kita harus menggambar poligon beraturan yang bersisi N-1. Jadi dalam contoh ini kita harus menggambar segitujuh beraturan. Setiap titik sudut dan titik tengah merepresentasikan masing-masing satu peserta.
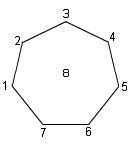
Selanjutnya, kita gambar garis horizontal yang menghubungkan 2 tim. Totalnya ada 3 garis. Setelah itu kita hubungkan 1 titik sudut yang tertinggal dengan menggambar garis antara titik tersebut dengan titik tengah sehingga kita lihat total ada 4 segmen garis. Setiap segmen garis ini merepresentasikan peserta-peserta yang saling berhadapan 1 sama lain pada putaran pertama.
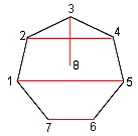
Dari gambar ini, kita bisa tulis (7,6), (1,5), (2,4), dan (3,8) akan dimainkan di putaran pertama.
Untuk menentukan pertandingan di tahap kedua, kita bisa rotasikan poligon ini dengan sudut 1/(N-1) dari sebuah lingkaran, atau kita putar sehingga sebuah titik sudut bergeser ke titik sudut sebelahnya. Nah, segmen-segmen garis yang baru akan kita peroleh dan ini merepresentasikan pasangan yang harus saling melawan di tahap kedua.
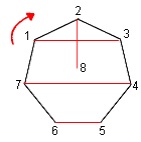
Dengan demikian, pada tahap kedua, (6,5), (7,4), (1,3), dan (2,8) akan saling berhadapan.
Kita bisa teruskan memutar poligon ini hingga ia kembali ke posisinya semula.
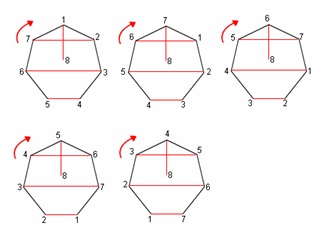
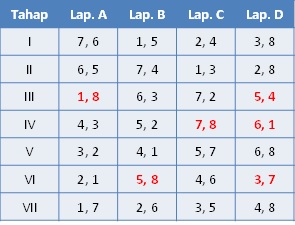
Perhatikan di langkah terakhir pada gambar, satu rotasi lagi akan mengembalikan poligon ke posisinya semula. Jika A, B, C, dan D merupakan nama lapangan yang akan digunakan pada waktu yang bersamaan dalam suatu tahap, kita bisa susun hasil pengaturan jadwal turnamen ini dalam bentuk tabel.

Namun kita lihat bahwa peserta No. 8 selalu bermain di lapangan D. Jika ini menjadi masalah, kita bisa saja menukar posisi lapangan pertandingan beberapa peserta sehingga setiap peserta pernah bermain di setiap lapang setidaknya sebanyak 1 kali.
Bagaimana jika jumlah peserta yang bertanding ganjil? Silakan coba atur sendiri. Caranya mirip seperti pengaturan pada jumlah peserta genap. Namun kali ini ada N tahap yang harus dimainkan dan setiap peserta setidaknya akan absen bermain pada salah satu tahap. Selamat mencoba! :)
Catatan:
Tulisan ini merupakan saduran bebas dari salah satu artikel berbahasa Inggris di http://nrich.maths.org/ tentang cara pengaturan jadwal sebuah turnamen.
Bahan bacaan:
Penulis:
Ahmad Ridwan T. Nugraha, peneliti fisika, alumnus ITB dan Tohoku University.
Kontak: art.nugraha(at)gmail(dot)com.



