Simetri dalam Matematika dan Sains

Alam memberikan contoh yang berlimpah akan fenomena-fenomena simetri. Sebagai contoh, dengan mengiris buah apel secara melintang, kita akan menemukan bahwa pusat apel memiliki simetri radial berbentuk bintang. Kupu-kupu memiliki sayap dengan detail pola yang simetris antara sayap kanan dan kiri, disebut juga dengan simetri bilateral. Daun-daun lidah buaya (Aloe vera) menyusun dirinya dengan pola yang dikenal sebagai spiral Fibonacci. Susunan daun-daun ini membentuk sudut 137,5 derajat antara lapisan atas dan lapisan bawahnya sehingga setiap daun tidak saling tindih ataupun menghalangi untuk mendapatkan sinar matahari.

Contoh-contoh simetri yang dapat ditemukan di alam: (a) simetri radial berbentuk bintang pada buah apel, (b) simetri bilateral pada sayap kupu-kupu, (c) simetri spiral Fibonacci pada daun lidah buaya.

Di dalam matematika, suatu benda dikatakan memiliki sifat simetris jika sifat benda tersebut tidak berubah setelah dikenakan operasi simetri.

Kita akan bahas beberapa contoh operasi simetri dengan fokus pada molekul agar memudahkan pemahaman.

Operasi identitas ($latex E$): Operasi ini berarti tidak melakukan perubahan apapun.
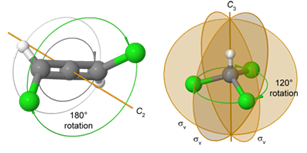
Operasi rotasi ($latex C_n$): Jika suatu molekul memiliki jenis simetri ini, posisi atom-atomnya tidak berubah setelah mengalami rotasi sebesar $latex 360^\circ / n$.

Contoh molekul yang memiliki simetri C2 dan C3 karena setiap molekul tetap identik saat diputar masing-masing sebesar 360∕2 = 180 derajat dan 360∕3 = 120 derajat dari sumbu rotasi.

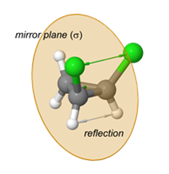
Operasi pencerminan/refleksi ($latex \sigma$): Molekul tetap identik setelah dicerminkan terhadap sebuah bidang tertentu.

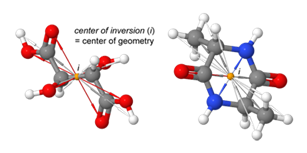
Operasi inversi ($latex i$): Operasi inversi dilakukan dengan mengambil satu atom pusat, kemudian posisi atom lain berpindah dari r → –r. Contoh molekul yang memiliki simetri inversi adalah asam tartat dan dimer dari D/L-alanin.

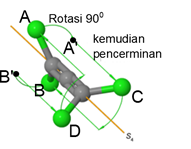
Operasi rotasi-refleksi ($latex S_n$): Operasi $latex S_n$ dilakukan dengan dua tahap, yaitu melakukan rotasi $latex C_n$ kemudian melakukan operasi pencerminan $latex \sigma$ pada sumbu yang tegak lurus dengan sumbu rotasi. Contoh molekul yang memiliki simetri rotasi-refleksi adalah tetra-kloralin ($latex \textrm{C}_3\textrm{Cl}_4$).

Pada ilustrasi operasi rotasi-refleksi ini mula-mula kita melakukan rotasi 90 derajat (C4) terhadap dua atom A→A' dan B→B', kemudian mencerminkannya hingga A' dan B' berhimpit dengan C dan D. — Pada ilustrasi operasi rotasi-refleksi ini mula-mula kita melakukan rotasi 90 derajat (C4) terhadap dua atom A→A’ dan B→B’, kemudian mencerminkannya hingga A’ dan B’ berhimpit dengan C dan D.

Setelah mengetahui bermacam-macam operasi simetri sederhana, kita mungkin bertanya apa kegunaannya? Dalam artikel ini akan dijelaskan dua buah saja aplikasi pemakaian operasi simetri dalam analisis matematis dan fisis.

Menyederhanakan perhitungan

Misalkan kita dihadapkan pada permasalahan integral seperti berikut: $latex \int_{-b}^{b} \sin x ~\textrm{d}x$. Kita mungkin bisa menghitung integral tersebut secara manual,

$latex \int_{-b}^{b} \sin x ~\textrm{d}x = -\cos b + \cos (-b) = 0$.

Akan tetapi, dengan mengingat bahwa fungsi sin(x) merupakan fungsi ganjil, yaitu sin(-x) = -sin(x), kita dapat melakukan operasi pencerminan terhadap sumbu-y pada daerah x = –b sampai x = 0 seperti diilustrasikan pada gambar di bawah:

$latex \int_{-b}^{0} \sin x ~\textrm{d}x \xrightarrow{\sigma_y} -\int_{0}^{b} \sin x ~\textrm{d}x$

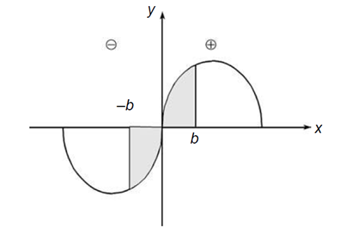
Dengan demikian,

$latex \int_{-b}^{b} \sin x ~\textrm{d}x = \int_{-b}^{0} \sin x ~\textrm{d}x + \int_{0}^{b} \sin x ~\textrm{d}x$

$latex \int_{-b}^{b} \sin x ~\textrm{d}x = – \int_{0}^{b} \sin x ~\textrm{d}x + \int_{0}^{b} \sin x ~\textrm{d}x = 0$

Kita lihat bahwa dengan menggunakan operasi simetri, perhitungan yang melibatkan fungsi-fungsi genap dan ganjil yang mungkin kompleks jadi dapat disederhanakan.

Menentukan polarisasi molekul (momen dipol)

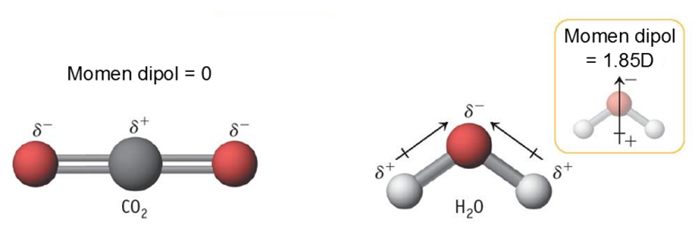
Di dalam suatu molekul, kerapatan elektron tidaklah merata. Elektron biasanya lebih menyukai atom yang lebih positif sehingga terjadi polarisasi (pengutuban) dalam molekul. Fenomena ini sangat penting saat material berinteraksi dengan lingkungan sekitar, contohnya cahaya. Molekul yang mengalami polarisasi, atau disebut molekul polar, dapat merespon cahaya, sedangkan molekul yang tidak mengalami pengutuban, disebut juga molekul nonpolar, tidak merespon cahaya.

Untuk membedakan mana molekul yang bersifat polar dan nonpolar, kita dapat menggunakan analisis simetri. Salah satu syarat molekul memiliki momen dipol adalah molekul tersebut tidak memiliki simetri inversi ($latex i$). Bila molekul memiliki simetri inversi, elektron-elektron di pusat atom terbagi sama kuat di kedua kutub sehingga tidak terjadi polarisasi, hal ini terjadi pada $latex \textrm{CO}_2$. Contoh molekul yang memiliki momen dipol adalah air, dengan oksigen bersifat lebih negatif daripada hidrogen.

Masih banyak lagi kegunaan analisis simetri ini di dalam dunia sains. Mulai dari dunia partikel yang terkecil hingga galaksi yang sangat besar, semua memiliki simetri dan akan sangat asyik untuk dipelajari. Keindahan simetri secara lebih mendalam dapat dinikmati dengan belajar teori grup (Group Theory).

Bahan bacaan:

Penulis:
Eddwi Hesky Hasdeo, mahasiswa/asisten peneliti di Departemen Fisika, Tohoku University, Jepang.
Kontak: heskyzone(at)gmail(dot)com.

Simetri dalam Matematika dan Sains