Mengenal Fisika Nonlinear

Fisika nonlinear adalah salah satu cabang fisika yang terkait dengan fenomena alam yang tidak dapat dijelaskan dengan persamaan linear maupun hukum alam yang linear. Fisika nonlinear membawa sekumpulan ide mendasar dan hasil-hasil yang mengejutkan. Akan tetapi, tidak seperti mekanika kuantum dan relativitas, bidang fisika nonlinear ini mencakup sistem pada seluruh ukuran dan benda-benda untuk semua kecepatan. Oleh karena itu, fisika nonlinear memiliki aplikasi yang sangat luas dalam kehidupan manusia sehari-hari. Di antara fenomena yang terkait fisika nonlinear adalah fraktal, chaos, pembentukan pola, dan sistem kompleks.

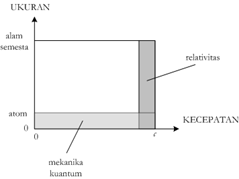
Domain mekanika kuantum dan relativitas. Fisika nonlinear mencakup semuanya.

Nonlinearitas

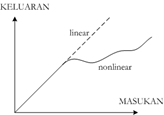
Sebuah sistem bersifat nonlinear jika keluaran dari sistem tidak sebanding dengan masukannya. Contohnya, kristal dielektrik dikatakan nonlinear jika keluaran intensitas cahaya tidak sebanding dengan intensitas cahaya datang. Dalam kehidupan sehari-hari, sistem penilaian ujian yang digunakan seorang profesor juga bersifat nonlinear jika tingkat nilai yang diperoleh oleh siswa tidak meningkat secara linear sebagai fungsi dari jumlah jam belajar siswa tersebut.

Tidak sulit bagi kita untuk melihat bahwa nonlinearitas merupakan kejadian yang lebih umum daripada linearitas. Dalam bentuk persamaan matematis, kita bisa nyatakan

(1)\quad \displaystyle\frac{dx}{dt} = a x^\alpha

dengan a dan α sebagai suatu konstanta. Persamaan ini menyatakan bahwa laju pertambahan sebuah besaran x(t) sebanding dengan nilainya saat itu yang dipangkatkan oleh bilangan α. Dari semua pilihan yang mungkin untuk nilai α, solusi dari persamaan (1) itu bersifat linear dalam variabel t jika α nol. Sementara itu, untuk nilai yang lain, x(t) menjadi fungsi nonlinear dari t.

Faktanya, hampir seluruh sistem yang diketahui di alam ini ternyata bersifat nonlinear ketika masukan darinya bernilai cukup besar. Contoh yang terkenal dan mudah dipahami adalah pegas. Ketika simpangan dari pegas semakin besar, hukum Hooke tidak berlaku lagi dan pegas tersebut menjadi osilator nonlinear. Contoh lainnya adalah bandul sederhana, hanya ketika sudut simpangan dari bandul cukup kecil, baru bisa anggap kelakuannya linear. Ada perbedaan kualitatif yang penting dari kelakuan sistem pada daerah linear dan juga daerah nonlinearnya. Periode osilasi bandul tidak bergantung pada amplitudo (simpangan maksimum) untuk daerah linear, tetapi periode itu akan bergantung pada amplitudo untuk daerah nonlinear.

Secara matematis, tanda yang jelas dari suatu sistem nonlinear adalah tidak berlakunya prinsip superposisi yang menyatakan bahwa jumlah dua buah solusi dari persamaan yang menggambarkan sistem juga akan menjadi solusi persamaan tersebut. Konsekuensi fisisnya, dalam sistem nonlinear ternyata kelakuan sistem secara menyeluruh itu akan lebih dari sekedar jumlah setiap bagiannya.

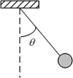
Ada dua jalan yang menyebabkan prinsip superposisi itu tidak berlaku. Pertama, persamaannya itu sendiri yang nonlinear. Sebagai contoh, persamaan gerak untuk massa titik dalam sebuah bandul sederhana diberikan oleh

(2)\quad \displaystyle\frac{d^2\theta}{dt^2} + (g/L) \sin \theta = 0

dengan Ө adalah sudut antara garis vertikal dan bandul, g adalah percepatan gravitasi, dan L adalah panjang bandul tersebut.

Sangatlah mudah untuk kita tunjukkan, jika Ө₁(t) dan Ө₂(t) masing-masing adalah solusi dari persamaan (2), maka jumlah Ө₁(t) + Ө₂(t)tidak akan menjadi solusi dari persamaan tersebut, sebuah konsekuensi dari fakta sederhana bahwa sin Ө₁ + sin Ө₂ tidak sama dengan Ө₁ + Ө₂. Akibatnya, persamaan (2) adalah persamaan nonlinear berdasarkan keberadaan suku nonlinear sin Ө. Di sisi lain, ketika Ө cukup kecil, kita bisa mengganti sin Ө dengan Ө sehingga persamaan tersebut menjadi linear dan prinsip superposisi akan berlaku.

Kedua, persamaannya boleh jadi linear tetapi batasannya tidak diketahui atau selalu berubah. Sebagai contoh, dalam permasalahan pembentukan pola, kita bisa mencoba untuk menentukan bentuk dan pergerakan dari permukaan tunggal yang memisahkan 2 buah cairan yang saling tertekan satu sama lain. Medan tekanan P pada setiap cairan dapat dinyatakan dalam persamaan Laplace yang merupakan persamaan linear. Akan tetapi, superposisi dari dua solusi permasalahan tersebut mengandung suku batas yang berbeda sehingga tidak mencerminkan solusinya.

Nonlinearitas dari sebuah sistem menjadikan sistem yang kita tinjau sangat nontrivial dan analisisnya cukup sulit. Contoh:

Untuk sebuah sistem nonlinear, gangguan berupa perubahan kecil pada kondisi awal dapat menghasilkan perubahan sifat yang sangat besar dari sistem pada waktu selanjutnya. Hal ini membuat perilaku dari sistem nonlinear menjadi sangat kompleks (seperti halnya kasus chaos).
Jika persamaan-persamaan yang menggambarkan sistem telah diketahui, kegagalan prinsip superposisi membawa kita pada teknik transformasi Fourier. Tidak ada metode sistematis yang serupa dengannya dalam pemecahan persamaan nonlinear. Sebagai contoh, metode hamburan terbalik dalam teori soliton hanya bisa diaplikasikan untuk sebuah subhimpunan dari sistem yang terintegrasi, dan belum ada cara untuk mengetahui sistem terintegrasi mana yang mempan terhadap metode ini.
Dalam banyak kasus, dari mulai batasan sederhana model pertumbuhan fraktal sampai dengan beberapa contoh dalam sistem kompleks seperti bidang ekonomi, persamaan yang menggambarkan sistem tersebut ternyata banyak yang belum diketahui, atau bahkan tidak ada.

Seluruh komplikasi tersebut menyebabkan penggunaan komputer menjadi sangat penting dalam pembahasan sistem nonlinear karena komputer dapat digunakan untuk melakukan perhitungan rumit, simulasi langsung, dan visualisasi yang sederhana. Berikut ini kita akan berikan satu contoh untuk sistem nonlinear berupa chaos.

Chaos adalah bahasa teknis dari sebuah fenomena sistem nonlinear yang kelakuannya sangat bergantung secara sensitif pada kondisi awalnya. Penggunaan kata chaos di sini tentu berbeda dengan penggunaannya dalam kehidupan sehari-hari yang sering diartikan sebagai “kekacauan yang menjadi-jadi”. Perbedaan konteks ini mirip seperti penggunaan kata “usaha” yang maknanya tidak sama dalam fisika dan bahasa.

Chaos telah diteliti oleh Henri Poincaré pada akhir abad ke-19 dan dilanjutkan oleh sejumlah matematikawan. Maraknya pembahasan tentang chaos akhir-akhir ini dimulai pada penghujung tahun 1970-an, yaitu ketika Mitchell Feigenbaum menemukan sifat umum dari beberapa pemetaan sederhana, yang didahului oleh pekerjaan Edward Lorenz terkait perkiraan cuaca. Tidak semua sistem nonlinear bersifat chaotic, tetapi fenomena chaos terjadi pada banyak sekali kasus riil maupun matematis, seperti pada tetesan air dari kran, rangkaian elektronik, konveksi termal pada cairan, reaksi kimia, bahkan detak jantung manusia.

Tanda dari suatu chaos dalam sebuah sistem disipatif adalah keberadaan suatu atraktor/penarik asing (strange attractor) dalam ruang fase, yang merupakan sebuah fraktal. Berkebalikan dengan itu, atraktor biasa (ordinary attractor) yang muncul dalam sistem tanpa chaos memiliki struktur sederhana dan dimensi yang integral. Akan tetapi fraktal dan chaos sebenarnya saling berkaitan, walaupun belum sepenuhnya dipahami.

Ada dua temuan penting dari sistem chaos:

Dalam pengaruh chaos, kelakuan sebuah sistem deterministik akan tampak acak. Sistem deterministik adalah sebuah sistem yang masa depannya dapat diketahui. Fakta ini memaksa setiap eksperimentalis agar memeriksa ulang data mereka untuk menentukan apakah suatu kelakuan acak berkaitan dengan derau (noise) dari data atau justru sistem deterministik yang bisa diprediksi.
Sistem-sistem nonlinear dengan hanya sedikit derajat kebebasan juga bisa bersifat chaos dan tampak sangat kompleks. Namun fakta ini memberikan harapan bahwa kelakuan kompleks yang teramati dalam banyak sistem riil dapat memiliki sebuah titik asal yang sederhana dan bahkan mungkin terlihat dengan jelas.

Meskipun kebanyakan chaos tampak sebagai suatu bentuk osilasi nonlinear yang seolah tidak aturannya, tetapi banyak pula sistem chaos yang ternyata dapat dirumuskan sebagai suatu pemetaan sederhana dari nilai deret mula-mula ke deret selanjutnya. Untuk kasus satu dimensi, kita dapat nyatakan

x_{n+1} = f(x_n)

dengan nilai variabel x_n dibatasi pada interval [0,1]. Pemetaan tertentu sesuai persamaan tersebut akan menghasilkan bentuk chaos pada grafik {x_n} terhadap n.

Ada 3 contoh pemetaan sederhana yang akan diberikan di sini yang dapat menghasilkan pola chaos, yaitu

Pemetaan logistik (logistic map)
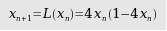
Pemetaan tenda (tent map)
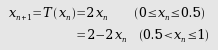
Transformasi biner (Bernoulli shift)

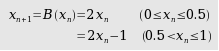
Kita bisa memplot x_n terhadap n setelah menghitung nilainya untuk masing-masing pemetaan. Sebagai contoh untuk nilai awal x₀ = 0,33, kita dapatkan pemetaan logistik, pemetaan tenda, dan transformasi biner seperti pada gambar.

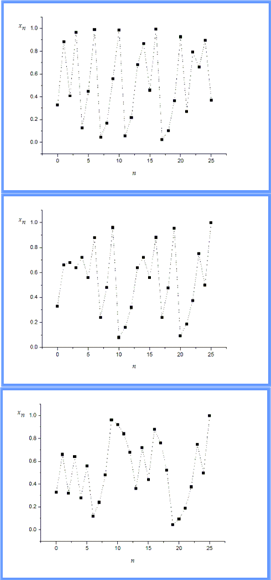
Perhatikan bahwa deretan angka yang tampak rumit ternyata dapat dibuat polanya dengan aturan pemetaan tertentu. Upaya seperti ini merupakan salah satu ranah fisika nonlinear agar hukum alam dapat diperoleh untuk fenomena-fenomena yang kompleks sekalipun.

Bahan bacaan:

Penulis:
Ahmad Ridwan T. Nugraha, peneliti fisika, alumnus ITB dan Tohoku University.
Kontak: art.nugraha(atgmail(dot)com

Mengenal Fisika Nonlinear