Banyak struktur ruang di alam ini dihasilkan dari penyusunan ulang komponen-komponen yang identik dalam jumlah besar. Dua proses yang paling sederhana dari penyusunan tersebut adalah keteraturan (regularity) dan keteracakan (randomness). Berdasarkan prinsip keteraturan, komponen-komponen terkecil dari suatu struktur dapat menyusun diri mereka sendiri dalam sebuah mode periodik atau kuasiperiodik menghasilkan bentuk semacam kristal atau logam, hingga formasi prajurit dalam suatu parade. Dari prinsip keteracakan, kita bisa ambil contoh distribusi gas dan pertumbuhan rambut binatang yang prosesnya berlangsung secara acak.
Di antara dua ekstrem keteraturan dan keteracakan, terdapat prinsip “kemiripan diri” (self-similarity) yang membawa kita pada sebuah struktur yang disebut dengan fraktal. Pada fraktal, ketika bagian dari suatu sistem membesar dengan perbesaran yang sama pada berbagai arah, bentuk tersebut akan menyerupai bentuk keseluruhannya. Ciri khas fraktal di sini adalah memiliki dimensi dalam bentuk pecahan.
Kita bisa melihat dimensi fraktal berupa pecahan pada salah satu contoh fraktal seperti segitiga Sierpinski. Untuk membentuk segitiga Sierpienski, pada langkah pertama (n = 0), kita memiliki sebuah segitiga sama sisi yang masing-masing sisinya bernilai 1 satuan. Pada langkah berikutnya (n = 1), kita potong seluruh bagian tengah segitiga tersebut oleh suatu bentuk segitiga terbalik. Pada n = 2, kita lakukan hal yang sama untuk setiap segitiga yang terbentuk dari langkah sebelumnya. Proses tersebut diulang terus-menerus sampai n menuju tak hingga. Himpunan segitiga pada langkah terakhir (n mendekati tak hingga) adalah segitiga Sierpinski. Setiap bagian kecil dari segitiga Sierpinski memiliki bentuk yang serupa seperti keseluruhannya.

Dimensi benda yang umum dalam kehidupan sehari-hari merupakan dimensi dalam ruang Euclid, yakni 0, 1, 2, dan 3. Dimensi dapat dibayangkan sebagai sebuah ukuran jumlah titik-titik yang sedang ditinjau. Konsep ini secara matematis mungkin tampak ganjil. Akan tetapi, garis paling tipis sekalipun memiliki tak hingga banyaknya titik sehingga sangat jelas bahwa suatu permukaan atau suatu bidang tentu tampak “lebih besar” dari sebuah garis atau kurva, seperti halnya suatu ruang “lebih besar” dari sebuah permukaan. Inilah alasan utama pemberian label dimensi 0 untuk titik, 1 untuk garis, 2 untuk bidang, dan 3 untuk ruang.
Dengan dimensinya yang berupa pecahan, fraktal memiliki bentuk semacam “transisi” antara benda-benda yang berdimensi sesuai definisi Euclid. Segitiga Sierpinski dapat dipandang sebagai transisi dari bidang menuju garis sehingga dimensinya berada di antara 1 dan 2, yaitu sekitar 1,58. Nilai ini dapat diperoleh dengan menggunakan definisi dimensi Hausdorf:
N_{\varepsilon} \approx \varepsilon^{-D}
atau
D = \displaystyle \lim_{\varepsilon \rightarrow \infty} \left( - \frac{\log N_{\varepsilon}}{\log \varepsilon}\right)
dengan Nɛ adalah jumlah objek terkecil yang masing-masing berukuran linear ɛ, dan D adalah dimensi objek. Sebagai contoh penerapan definisi Hausdorf itu, kita bisa lihat kembali gambar segitiga Sierpinski. Pada kasus ini, Nɛ = 3n untuk ɛ = 2-n. Kita bisa hitung log Nɛ / log ɛ = (n log 3) / (–n log 2) sehingga dimensi segitiga Sierpinski adalah
D = \displaystyle\frac{\log 3}{\log 2} \approx 1,58 .
Konsep fraktal dalam fisika memiliki aplikasi yang sangat luas, dari masalah fluida hingga rangkaian listrik dalam elektronika. Keberadaan fraktal yang ternyata ada dalam hampir seluruh sudut alam dan sistem matematis pertama kali dikenal setelah Benoit Mandelbrot memublikasikan bukunya yang berjudul The Fractal Geometry of Nature pada tahun 1982. Dalam tulisan ini, kita coba menggunakan konsep fraktal, khsusunya perhitungan dimensi fraktal, untuk menentukan kualitas resapan air oleh bahan-bahan berserat yang memiliki massa tertentu.
Dari definisi kerapatan massa, secara intuitif kita tentukan dimensi fraktal suatu material melalui hubungan
m = kRD,
dengan m, R, D, dan k berturut-turut adalah massa fraktal, ukuran linear berdimensi satu (misalnya panjang/lebar/diameter), dimensi fraktal, dan suatu konstanta (dalam hal ini adalah kerapatan massa). Pada ruang Euclid, nilai D adalah dimensi bilangan bulat. Dengan demikian, D = 1 memberikan k = λ, yaitu massa per satuan panjang; D = 2 memberikan k = σ, yaitu massa per satuan luas; dan D = 3 memberikan k = ρ atau massa per satuan volum. Untuk menentukan dimensi fraktal, kita gunakan hubungan logaritmik dari massa terhadap dimensi:
log m = log k + D log R .
Kualitas resapan air oleh suatu bahan berserat atau berpori biasanya tergantung pada ukuran dan geometri bahan tersebut. Geometri suatu benda sangat terkait dengan dimensinya. Oleh karena itu, kemampuan bahan untuk menyerap cairan bisa saja diasumsikan bergantung langsung pada dimensi, yang secara umum berdimensi fraktal (pecahan). Untuk menguji asumsi ini, kita bisa lakukan percobaan sederhana dengan beberapa macam bahan kertas, seperti kertas HVS, kertas manila, koran bekas, dan kertas stensil.
Lembaran kertas pada dasarnya adalah benda berdimensi dua. Untuk dijadikan fraktal (berdimensi pecahan), bahan-bahan tersebut diremas-remas sehingga menyerupai bola. Pada percobaan ini dibutuhkan beberapa buah data. Oleh karena itu, setiap jenis bahan tersebut dipotong menjadi beberapa ukuran berbeda. Setelahnya, kita bisa bentuk kertas seperti bola dengan ukuran yang bervariasi pula.

Data yang dibutuhkan untuk menentukan dimensi “fraktal kertas” yang telah dibuat adalah massa dan diameternya. Setiap bola-bola kertas diukur massanya, lalu diukur diameternya sebanyak dua kali pada tempat yang berbeda (semakin banyak semakin baik). Kedua diameter hasil pengukuran itu lalu dirata-ratakan. Diameter rata-rata inilah yang digunakan untuk pengolahan data. Setelah data massa (m) dan diameter (R) bola-bola kertas diketahui, kita plot fungsi log m terhadap log R. Sesuai dengan hubungan log m = log k + D log R, gradien atau kemiringan dari grafik akan menunjukkan dimensi fraktal kertas tersebut.
Setelah dimensi fraktal kertas diketahui, kita ingin melihat seberapa besar daya serap bahan terhadap cairan tertentu. Data yang dibutuhkan adalah banyaknya cairan (air) yang diserap oleh bahan tersebut. Salah satu cara yang paling mudah adalah dengan mengukur massa air yang terserap. Semua fraktal kertas dicelupkan ke dalam air beberapa saat, kemudian diukur lagi massanya. Massa air yang terserap adalah massa fraktal kertas setelah menyerap air dikurangi massa fraktal kertas saat kering. Dengan membuat grafik lagi, massa air (ma) yang diserap dapat dibandingkan terhadap diameter bola (R). Kita bisa perhatikan contoh grafik penentuan dimensi fraktal dan hubungan massa air terhadap diameter untuk kertas HVS.
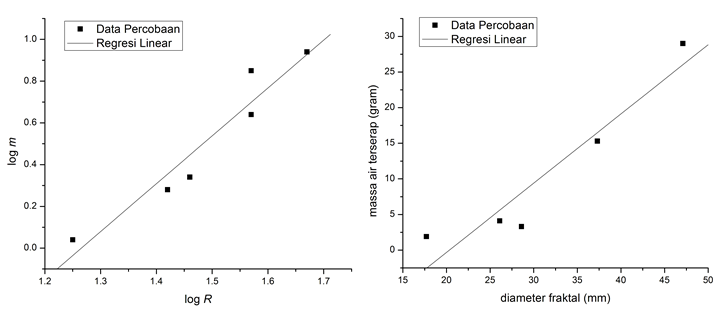
Dari grafik massa air terserap versus diameter fraktal kertas, ternyata ada hubungan linear sehingga kita bisa tuliskan persamaan:
ma = gR + C,
dengan g adalah gradien resapan dan C adalah konstant regresi. Secara keseluruhan, dimensi fraktal dan gradien resapan yang diperoleh pada eksperimen untuk bahan yang berbeda dapat dilihat pada tabel.
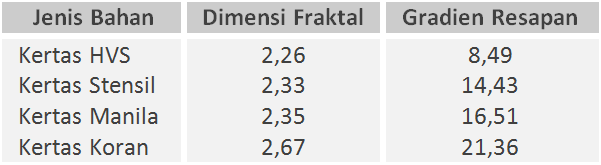
Dari penentuan dimensi fraktal, kita dapat melihat dimensi fraktal kertas yang diremas bernilai antara 2 (bidang) dan 3 (ruang), sesuai dengan anggapan dasar bahwa kertas mengalami semacam perubahan dimensi bidang berdimensi 2 menuju bentuk bola berdimensi 3. Hasil yang menarik diperoleh pada percobaan pengukuran daya serap bahan terhadap air, dimensi fraktal ternyata berbanding lurus dengan gradien resapan air oleh fraktal kertas. Semakin besar dimensi fraktal, semakin besar pula gradien resapannya. Artinya, dimensi fraktal cukup memengaruhi kualitas bahan berserat dalam menyerap cairan.
Berdasarkan percobaan yang telah dilakukan, kertas koran terlihat memiliki dimensi fraktal yang paling besar dibandingkan dengan kertas manila, stensil, ataupun HVS. Bisa jadi, dimensi fraktal ini yang menjadi alasan mengapa kita lebih mudah membersihkan jendela yang kotor dengan bantuan koran bekas. Meskipun tampak tidak saling terkait, beberapa penelitian belakangan, misalnya dari Journal of Applied Geophysics (2012) dan Powder Technology (2011), menunjukkan ada hubungan yang erat antara porositas, permeabilitas, dan dimensi fraktal.
Bahan bacaan:
- http://majalah1000guru.net/2012/01/berkenalan-dengan-fraktal/
- http://dx.doi.org/10.1016/j.powtec.2011.10.053
- http://dx.doi.org/10.1016/j.jappgeo.2012.07.015
- Mandelbrot, The Fractal Geometry of Nature (1982).
Catatan:
Sebagian besar isi tulisan ini beserta percobaan yang terkandung di dalamnya pernah menjadi salah satu finalis pada Pekan Ilmiah Mahasiswa Nasional tahun 2007 ketika penulis masih berstatus mahasiswa S-1.
Penulis:
- Indra W. Fathona, dosen fisika di Universitas Telkom, alumnus ITB dan Hiroshima University.
Kontak: indrafathonah(at)gmail(dot)com. - Ahmad Ridwan T. Nugraha, peneliti fisika, alumnus ITB dan Tohoku University.
Kontak: art.nugraha(at)gmail(dot)com.



