Teman-teman pembaca majalah 1000guru pasti pernah lihat wadah penampungan air di sekitar tempat tinggalnya. Misalnya tangki yang digunakan untuk menampung air hujan atau toren yang digunakan sebagai sarana penyimpanan cadangan air. Yuk kita bermain sejenak dengan wadah air semacam ini sambil belajar konsep fisika yang sederhana.
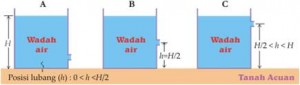
Perhatikan gambar di bawah. Misalkan saja kita punya beberapa wadah penampungan air dengan posisi lubang air yang berbeda pada dinding wadah. Nah, di antara gambar A, B, dan C, manakah yang jarak pancaran airnya paling jauh jika penutup lubang dibuka bersamaan?
Sekarang kita sedikit modifikasi posisi wadah penampungan air ini seperti pada gambar di bawah. Di antara gambar D dan E, manakah yang jarak pancaran airnya lebih jauh?
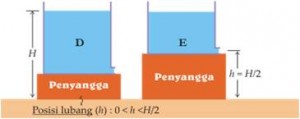
Intuisi kita mungkin mengatakan, “Pancaran air paling deras itu yang posisinya paling bawah sehingga seharusnya posisi itu yang memancarkan air paling jauh (gambar A dan D)!”
Eits, tunggu dulu! Ternyata intuisi kita tidak selalu tepat.
Jawaban yang benar justru adalah B dan E!
Mengapa bisa demikian? Alasan singkatnya adalah terkait prinsip Bernoulli. Teman-teman ketika belajar di sekolah menengah seharusnya pernah belajar prinsip tersebut. Prinsip ini menjelaskan bahwa peningkatan laju suatu fluida (cairan) yang alirannya bersifat tunak akan selalu diiringi dengan penurunan tekanan atau penurunan energi potensial dari fluida.
Secara matematis, prinsip Bernoulli dapat dituliskan sebagai persamaan Bernoulli, yaitu
$latex p + \rho g y + \frac{1}{2} \rho v^2 = $ tetap di manapun juga
Pada persamaan Bernoulli ini, p merupakan tekanan di suatu titik tertentu pada aliran fluida, ρ adalah massa jenis fluida, g percepatan gravitasi, y posisi titik aliran fluida diukur dari suatu acuan (misalnya tanah), dan v adalah laju fluida pada titik aliran yang sedang ditinjau.
Untuk memecahkan permasalahan yang diberikan di awal, kita harus tahu dulu besar kecepatan air yang memancar dari lubang pada ketinggian tertentu. Secara umum, kita bisa memanfaatkan persamaan Bernoulli dengan memisalkan salah satu titik di permukaan air (posisi paling atas) diberi label 1 dan titik pada lubang diberi label 2 sehingga persamaan Bernoulli dapat ditulis sebagai
$latex p_1 + \rho g y_1 + \frac{1}{2} \rho v_1^2 = p_2 + \rho g y_2 + \frac{1}{2} \rho v_2^2$
Permukaan air dan lubang air berhubungan langsung dengan udara luar sehingga tekanannya sama-sama tekanan udara luar:
$latex p_1 = p_2$
Nah, kita bisa sederhanakan persamaan Bernoulli dengan mencoret suku tekanan pada kedua ruas sehingga kita dapatkan:
$latex \rho g (y_1 – y_2) = \frac{1}{2} \rho (v_2^2 – v_1^2)$
Persamaan ini masih bisa disederhanakan lagi mengingat fluida di titik 1 (permukaan) dan titik 2 (posisi lubang) sama-sama berwujud “air” (misalnya air ledeng, air hujan) sehingga bisa kita coret lagi. Selain itu, kita bisa asumsikan air di titik 1 bergerak sangat lambat ketika jumlahnya berkurang (alias nilai v1 mendekati nol). Substitusikan pula ketinggian y1 dan y2 sesuai dengan soal, yaitu y1 = H dan y2 = h. Dengan demikian
$latex 2 g (H – h) = v_2^2$
Karena tinggal ada satu macam kecepatan saja, yaitu v2 (kecepatan air pada lubang), kita ganti simbolnya menjadi v, yang dapat dituliskan menjadi:
$latex v = \sqrt{2 g (H – h)}$
Dari hasil perhitungan persamaan Bernoulli tersebut, kita sekarang paham bahwa kecepatan air ditentukan oleh (H–h), yaitu kedalaman lubang diukur dari permukaan. Semakin dalam posisi lubang, semakin besar pula kecepatannya. Ini masih sesuai dengan salah satu petikan intuisi kita di awal bahwa, “Pancaran air paling deras itu yang posisinya paling bawah.” Akan tetapi, perhatikan pula bahwa semakin deras laju air tidaklah menjamin pancarannya akan paling jauh!
Untuk mendapatkan jawaban dengan lengkap, kita membutuhkan persamaan kinematika gerak parabola:
$latex x = v t \quad h = \frac{1}{2} g t^2$
x di sini adalah jarak tempuh pada arah mendatar, sedangkan h adalah ketinggian diukur dari tanah pada waktu tertentu (t). Dengan memanfaatkan rumus ini, waktu tempuh satu partikel air dari lubang untuk mencapai tanah
$latex t = \sqrt{\frac{2h}{g}}$
Substitusikan rumus kecepatan air dan waktu tempuh pada rumus jarak x:
$latex x = \sqrt{\frac{2h}{g}} \sqrt{2 g (H – h)}$
Pada akhirnya, jarak pancaran air ditentukan oleh rumus
$latex x = 2 \sqrt{h (H – h)}$
Nilai di dalam tanda akar bisa maksimum jika h = (H–h). Dengan kata lain, h = H/2. Itulah sebabnya jawaban dari permasalahan yang diberikan di awal tulisan ini adalah gambar B dan E.
Kesimpulannya, laju air paling deras bukan berarti jarak tempuhnya paling jauh. Pesan moralnya, intuisi kita terkadang dapat mengarahkan kepada keputusan yang keliru.
Catatan:
Tulisan ini diterbitkan ulang oleh penulis dengan beberapa perubahan dari tulisan lama di komunitas 102FM ITB.
Bahan bacaan:
- http://hyperphysics.phy-astr.gsu.edu/hbase/pber.html
- http://en.wikipedia.org/wiki/Bernoulli’s_principle
Penulis:
Ahmad Ridwan T. Nugraha, peneliti fisika, alumnus ITB dan Tohoku University.
Kontak: art.nugraha(at)gmail(dot)com.



